Tentukan kedudukan titik b terhadap garis ab – Bayangkan sebuah peta misterius yang hanya menunjukkan garis lurus, tanpa tanda atau petunjuk. Di tengah peta itu, terdapat sebuah titik yang diberi label ‘B’. Misi Anda: menentukan posisi titik ‘B’ terhadap garis yang ditandai ‘AB’. Apakah ‘B’ terletak di atas garis, di bawah garis, atau tepat di atas garis? Petualangan ini akan membawa kita menjelajahi dunia geometri, mengungkap rahasia titik dan garis, dan akhirnya menemukan jawaban atas teka-teki ‘B’ yang tersembunyi.
Dalam dunia geometri, titik dan garis merupakan elemen dasar yang membentuk berbagai bentuk dan ruang. Titik, seperti sebuah titik kecil yang tak berdimensi, mewakili lokasi di ruang, sedangkan garis merupakan kumpulan titik yang terhubung secara tak terhingga. Untuk memahami kedudukan titik ‘B’ terhadap garis ‘AB’, kita perlu memahami definisi titik dan garis, serta kemungkinan posisi titik terhadap garis.
Pengertian Titik dan Garis
Dalam dunia geometri, titik dan garis merupakan konsep dasar yang mendasari pemahaman tentang bentuk dan ruang. Titik dan garis adalah elemen fundamental yang saling terkait dan membentuk dasar untuk membangun berbagai bentuk geometri lainnya.
Pengertian Titik
Titik adalah objek dasar dalam geometri yang tidak memiliki dimensi. Artinya, titik tidak memiliki panjang, lebar, atau tinggi. Titik hanya memiliki posisi dalam ruang. Kita dapat membayangkan titik sebagai sebuah lokasi yang sangat kecil, yang hanya memiliki satu posisi tertentu. Titik biasanya dilambangkan dengan huruf kapital, seperti titik A, titik B, atau titik C.
Pengertian Garis
Garis adalah kumpulan titik-titik yang tak terhingga banyaknya yang tersusun secara berurutan dan memanjang ke kedua arah. Garis tidak memiliki ketebalan, hanya memiliki panjang. Garis dapat dibayangkan sebagai jejak yang dibentuk oleh sebuah titik yang bergerak secara terus menerus dalam satu arah. Garis biasanya dilambangkan dengan huruf kecil, seperti garis a, garis b, atau garis c.
Contoh Ilustrasi Titik dan Garis
Bayangkan sebuah papan tulis kosong. Saat Anda menorehkan ujung pensil ke papan tulis, Anda menciptakan sebuah titik. Titik ini merupakan representasi visual dari konsep titik dalam geometri. Sekarang, bayangkan Anda menggeser ujung pensil tersebut secara terus menerus di atas papan tulis. Jejak yang dihasilkan oleh ujung pensil tersebut adalah sebuah garis. Garis ini merupakan representasi visual dari konsep garis dalam geometri.
Kedudukan Titik terhadap Garis: Tentukan Kedudukan Titik B Terhadap Garis Ab
Dalam geometri, memahami kedudukan titik terhadap garis merupakan konsep dasar yang penting. Titik dan garis dapat memiliki hubungan yang beragam, dan memahami hubungan ini akan membantu kita dalam memecahkan berbagai masalah geometri.
Tiga Kemungkinan Kedudukan Titik terhadap Garis
Titik terhadap garis dapat memiliki tiga kemungkinan kedudukan, yaitu:
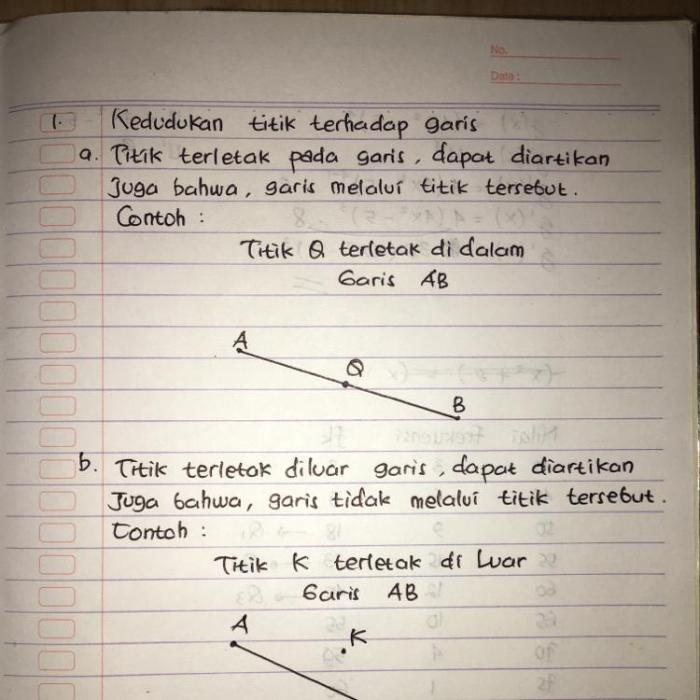
- Titik terletak pada garis
- Titik terletak di luar garis
- Titik terletak di dalam garis
Tabel Kedudukan Titik terhadap Garis
Berikut tabel yang merangkum tiga kemungkinan kedudukan titik terhadap garis, beserta ilustrasi gambarnya:
| Kedudukan Titik | Ilustrasi | Keterangan |
|---|---|---|
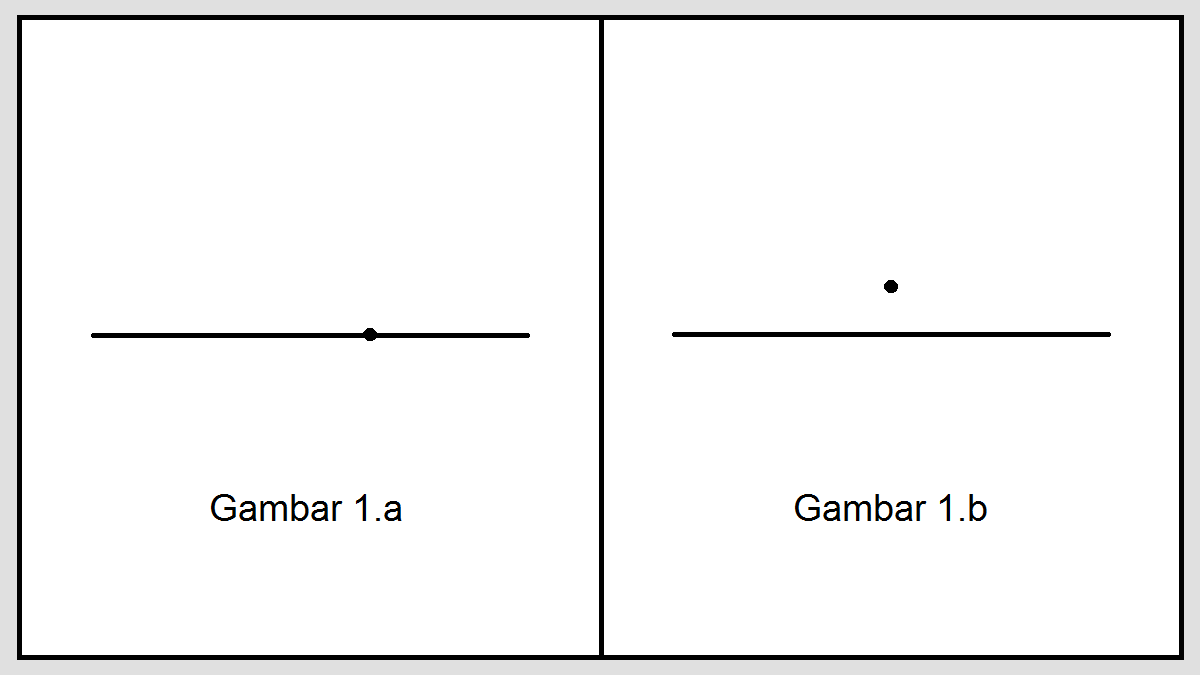
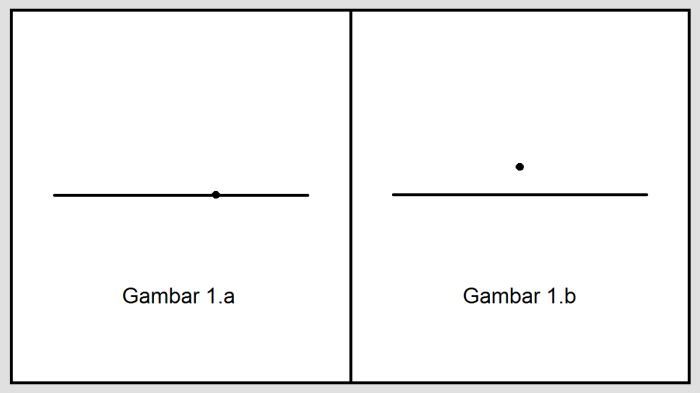
| Titik terletak pada garis | Bayangkan sebuah garis lurus. Titik A terletak tepat di atas garis tersebut. | Titik tersebut berada di atas garis lurus dan tepat bersinggungan dengan garis tersebut. |
| Titik terletak di luar garis | Bayangkan sebuah garis lurus. Titik B berada di sebelah kanan garis tersebut. | Titik tersebut berada di luar garis lurus dan tidak bersinggungan dengan garis tersebut. |
| Titik terletak di dalam garis | Bayangkan sebuah garis lurus. Titik C berada di tengah-tengah garis tersebut. | Titik tersebut berada di tengah-tengah garis lurus dan tidak bersinggungan dengan garis tersebut. |
Contoh Ilustrasi
Berikut adalah contoh ilustrasi untuk masing-masing kemungkinan kedudukan titik terhadap garis:
- Titik terletak pada garis: Bayangkan sebuah peta jalan. Titik A mewakili sebuah kota yang terletak tepat di atas jalan tol. Titik A berada pada garis yang mewakili jalan tol.
- Titik terletak di luar garis: Bayangkan sebuah lapangan sepak bola. Titik B mewakili posisi seorang pemain yang berada di luar garis lapangan. Titik B berada di luar garis yang mewakili lapangan.
- Titik terletak di dalam garis: Bayangkan sebuah garis lurus yang mewakili garis pantai. Titik C mewakili posisi sebuah pulau kecil yang terletak di tengah-tengah garis pantai. Titik C berada di dalam garis yang mewakili garis pantai.
Menentukan Kedudukan Titik B terhadap Garis AB
Dalam geometri analitik, menentukan kedudukan titik terhadap garis merupakan konsep penting yang membantu kita memahami hubungan spasial antara titik dan garis. Dalam pembahasan ini, kita akan fokus pada bagaimana menentukan kedudukan titik B terhadap garis AB dengan menggunakan koordinat titik. Pengetahuan ini bermanfaat dalam berbagai aplikasi, seperti menentukan posisi objek dalam ruang, menghitung jarak antara titik dan garis, serta memahami hubungan antara titik dan garis dalam berbagai model geometri.
Menentukan Kedudukan Titik B terhadap Garis AB dengan Koordinat Titik
Untuk menentukan kedudukan titik B terhadap garis AB, kita dapat menggunakan konsep gradien dan persamaan garis. Berikut langkah-langkahnya:
- Tentukan koordinat titik A dan B.
- Hitung gradien garis AB dengan rumus:
Gradien (m) = (yB – yA) / (xB – xA)
- Tentukan persamaan garis AB dengan menggunakan salah satu titik (A atau B) dan gradien yang telah dihitung. Persamaan garis dapat ditulis dalam bentuk persamaan garis lereng-titik:
y – yA = m(x – xA)
- Substitusikan koordinat titik B ke dalam persamaan garis AB. Jika persamaan tersebut terpenuhi, maka titik B terletak pada garis AB. Jika tidak, maka titik B tidak terletak pada garis AB.
Contoh Soal dan Penyelesaian
Misalkan kita ingin menentukan kedudukan titik B(3, 4) terhadap garis AB dengan titik A(1, 2).
- Koordinat titik A(1, 2) dan B(3, 4).
- Gradien garis AB:
m = (4 – 2) / (3 – 1) = 2 / 2 = 1
- Persamaan garis AB:
y – 2 = 1(x – 1)
y – 2 = x – 1
y = x + 1
- Substitusikan koordinat titik B(3, 4) ke dalam persamaan garis AB:
4 = 3 + 1
4 = 4
Persamaan tersebut terpenuhi, sehingga titik B(3, 4) terletak pada garis AB.
Flowchart Menentukan Kedudukan Titik B terhadap Garis AB
Berikut adalah flowchart yang menggambarkan langkah-langkah menentukan kedudukan titik B terhadap garis AB:
Gambar flowchart: [Flowchart menggambarkan langkah-langkah menentukan kedudukan titik B terhadap garis AB dengan simbol-simbol standar, seperti persegi panjang untuk proses, berlian untuk keputusan, dan panah untuk aliran data. Flowchart ini menunjukkan urutan langkah-langkah yang jelas, mulai dari input data hingga output keputusan tentang kedudukan titik B terhadap garis AB.]
Penerapan Kedudukan Titik terhadap Garis

Konsep kedudukan titik terhadap garis, yang telah kita pelajari sebelumnya, ternyata memiliki aplikasi yang luas dan bermanfaat dalam berbagai aspek kehidupan kita. Dari arsitektur hingga teknik, konsep ini berperan penting dalam perencanaan, desain, dan konstruksi berbagai objek dan infrastruktur.
Contoh Penerapan dalam Kehidupan Sehari-hari
Bayangkan Anda sedang berjalan di jalan raya. Anda berada pada suatu titik, dan jalan raya merupakan garis. Posisi Anda terhadap jalan raya dapat didefinisikan sebagai titik yang berada di atas, di bawah, atau tepat di atas garis jalan raya. Konsep ini sederhana namun memiliki implikasi penting, misalnya untuk menentukan jarak aman Anda dari kendaraan yang lewat.
Penerapan dalam Arsitektur dan Desain
Dalam arsitektur dan desain, konsep kedudukan titik terhadap garis berperan penting dalam penempatan elemen-elemen bangunan, seperti jendela, pintu, dan kolom. Arsitek menggunakan konsep ini untuk memastikan pencahayaan yang optimal, sirkulasi udara yang baik, dan estetika bangunan yang harmonis. Misalnya, penempatan jendela pada suatu titik yang tepat terhadap garis dinding dapat memaksimalkan cahaya alami yang masuk ke ruangan, sekaligus menciptakan pemandangan yang indah.
Penerapan dalam Teknik, Tentukan kedudukan titik b terhadap garis ab
Dalam teknik, konsep kedudukan titik terhadap garis memiliki aplikasi yang luas, terutama dalam bidang teknik sipil dan mekanik. Misalnya, dalam perencanaan jalan raya, konsep ini digunakan untuk menentukan posisi titik-titik penting seperti tikungan, persimpangan, dan jembatan. Dalam teknik mekanik, konsep ini diterapkan dalam desain mesin, di mana posisi komponen-komponen mesin yang tepat terhadap garis sumbu putar sangat penting untuk memastikan kinerja mesin yang optimal.
Contoh Kasus
Misalnya, Anda ingin membangun sebuah jembatan melintasi sungai. Jembatan tersebut harus dibangun pada titik-titik tertentu yang berada di atas permukaan sungai. Untuk menentukan titik-titik tersebut, Anda dapat menggunakan konsep kedudukan titik terhadap garis. Anda dapat menentukan garis sungai sebagai acuan, dan titik-titik di mana jembatan akan dibangun harus berada di atas garis sungai tersebut.