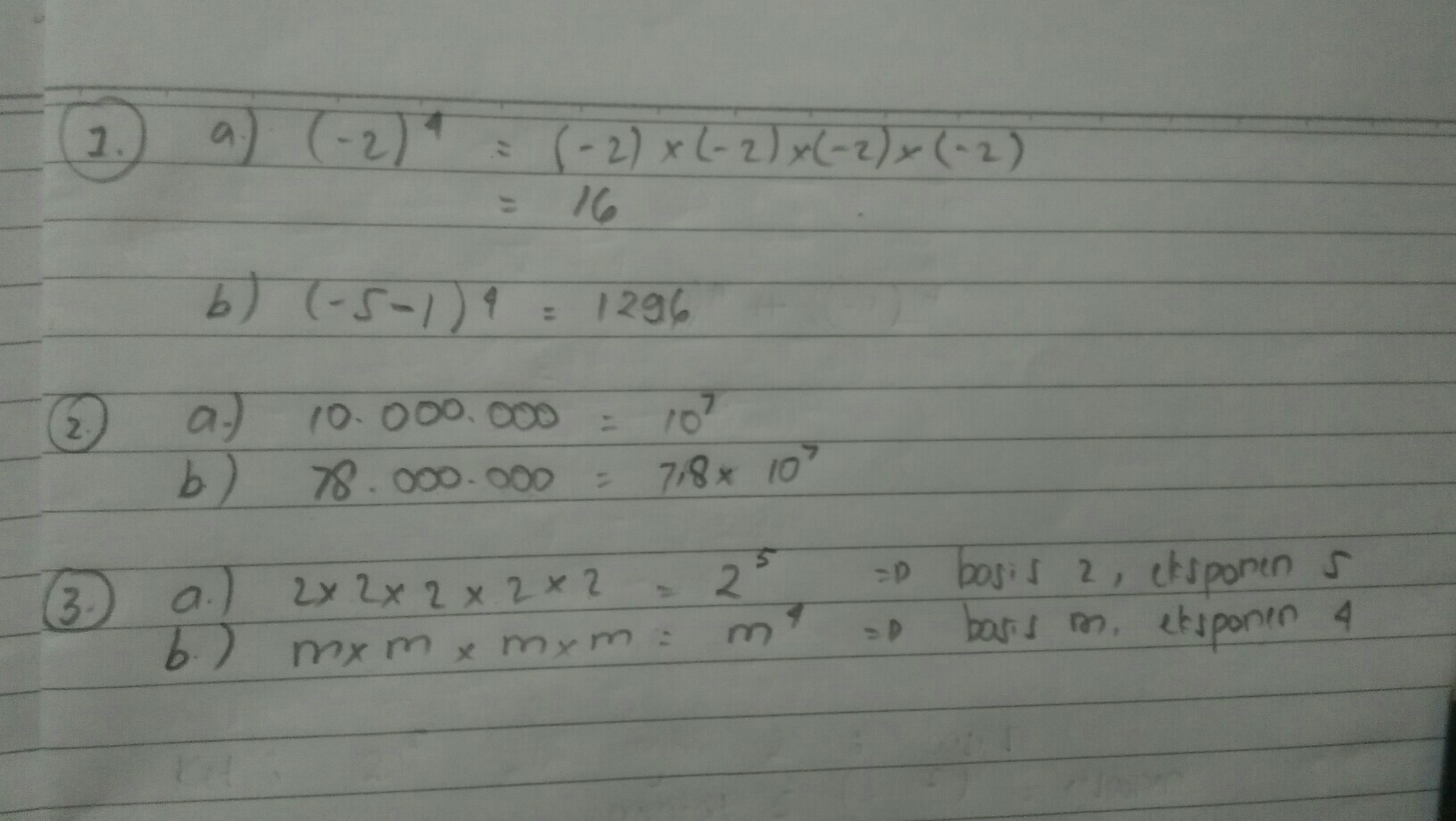Tentukan hasil pemangkatan bilangan berpangkat berikut – Yo, what’s up, mathletes! Ever wondered how those crazy exponents work when they’re stacked on top of each other? Well, get ready to unlock the secrets of “Tentukan Hasil Pemangkatan Bilangan Berpangkat: Kuasai Rumusnya!” We’re diving deep into the world of powers and exponents, where numbers get amplified like a rock concert.
Imagine you’re trying to calculate the volume of a super-sized cube. You’ve got the length, width, and height, but how do you crunch those numbers together? That’s where exponents come in, especially when those numbers are already raised to a power. This lesson is all about understanding the rules of the game, so you can conquer any exponent challenge that comes your way.
Pengertian Pemangkatan Bilangan Berpangkat
Bayangkan kamu sedang berpetualang di dunia matematika yang penuh teka-teki. Di sana, kamu menemukan sebuah ruangan gelap yang dipenuhi dengan angka-angka misterius. Di tengah ruangan, terukir sebuah simbol aneh: “x^y”. Apa gerangan arti simbol ini?
Simbol “x^y” adalah simbol dari pemangkatan bilangan berpangkat. Pemangkatan bilangan berpangkat adalah sebuah operasi matematika yang menggabungkan dua bilangan: bilangan pokok (x) dan pangkat (y). Bilangan pokok dikalikan dengan dirinya sendiri sebanyak pangkat.
Ilustrasi Pemangkatan Bilangan Berpangkat, Tentukan hasil pemangkatan bilangan berpangkat berikut
Untuk memahami konsep ini lebih dalam, bayangkan sebuah diagram sederhana. Misalkan kita punya bilangan pokok 2 dan pangkat 3.
Ilustrasi:
Di diagram ini, kita lihat bilangan pokok 2 dikalikan dengan dirinya sendiri sebanyak 3 kali (sesuai dengan pangkat). Hasilnya adalah 2 x 2 x 2 = 8. Jadi, 2^3 = 8.
Rumus Dasar Pemangkatan Bilangan Berpangkat
Nah, sekarang kita masuk ke bagian yang lebih menarik. Ada beberapa rumus dasar yang bisa kita gunakan untuk menghitung pemangkatan bilangan berpangkat:
| Rumus | Contoh |
|---|---|
| x^0 = 1 | 2^0 = 1 |
| x^1 = x | 3^1 = 3 |
| x^n = x * x * … * x (n kali) | 4^2 = 4 * 4 = 16 |
| (x^m)^n = x^(m*n) | (5^2)^3 = 5^(2*3) = 5^6 = 15625 |
| x^m * x^n = x^(m+n) | 2^3 * 2^2 = 2^(3+2) = 2^5 = 32 |
| x^m / x^n = x^(m-n) | 6^4 / 6^2 = 6^(4-2) = 6^2 = 36 |
Sifat-Sifat Pemangkatan Bilangan Berpangkat
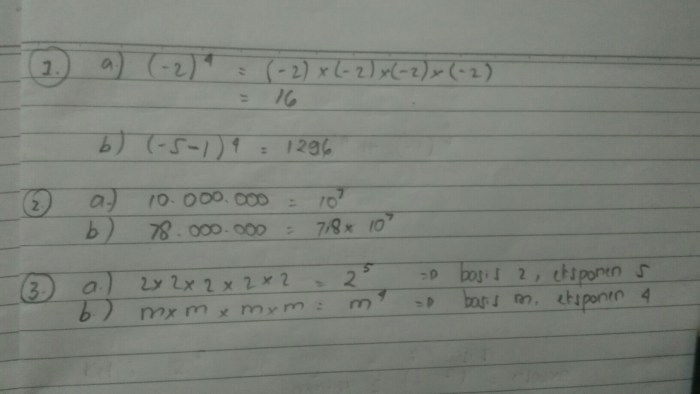
Bayangkan sebuah kotak misterius. Di dalamnya, tersimpan sebuah bilangan yang sedang bersembunyi, dibungkus oleh dua lapis kekuatan. Kekuatan pertama, seperti kunci yang membuka kotak, adalah pangkat pertama. Kekuatan kedua, seperti kunci rahasia yang menjaga harta di dalam, adalah pangkat kedua. Nah, bagaimana kita mengungkap rahasia di balik kotak ini? Dengan memahami sifat-sifat pemangkatan bilangan berpangkat, kita dapat menguraikan kekuatan-kekuatan yang tersembunyi di dalam kotak misterius ini.
Sifat-Sifat Pemangkatan Bilangan Berpangkat
Sifat-sifat pemangkatan bilangan berpangkat adalah aturan-aturan yang mengatur bagaimana bilangan berpangkat saling berinteraksi. Aturan-aturan ini menjadi kunci untuk membuka rahasia kotak misterius kita. Dengan menggunakan aturan ini, kita dapat mempermudah operasi pemangkatan dan menemukan hasil yang tepat.
-
Sifat 1: (am)n = am x n
Ketika pangkat bertemu pangkat, kekuatannya berlipat ganda. Misalnya, (23)2 = 23 x 2 = 26. Dalam kasus ini, pangkat pertama, 3, bertemu dengan pangkat kedua, 2, dan menghasilkan pangkat baru, 6. Ini seperti dua kunci yang membuka dua lapis kekuatan, menghasilkan kekuatan yang lebih besar.
-
Sifat 2: am x an = am + n
Ketika bilangan berpangkat yang sama bertemu, kekuatannya bersatu. Misalnya, 23 x 22 = 23 + 2 = 25. Dalam kasus ini, pangkat pertama, 3, dan pangkat kedua, 2, bergabung menjadi satu pangkat, 5. Ini seperti dua kunci yang membuka dua kotak yang sama, menggabungkan harta di dalamnya.
-
Sifat 3: am / an = am – n
Ketika bilangan berpangkat yang sama dibagi, kekuatannya berkurang. Misalnya, 25 / 22 = 25 – 2 = 23. Dalam kasus ini, pangkat pertama, 5, dikurangi oleh pangkat kedua, 2, menghasilkan pangkat baru, 3. Ini seperti satu kunci yang membuka satu kotak, dan kemudian kunci lainnya digunakan untuk mengambil beberapa harta di dalamnya, mengurangi jumlah harta yang tersisa.
-
Sifat 4: (a x b)n = an x bn
Ketika dua bilangan yang berbeda dikalikan dan dipangkatkan, kekuatannya berlaku pada masing-masing bilangan. Misalnya, (2 x 3)2 = 22 x 32 = 4 x 9 = 36. Dalam kasus ini, pangkat 2 diterapkan pada kedua bilangan, 2 dan 3, secara terpisah. Ini seperti dua kunci yang membuka dua kotak yang berbeda, mengungkap harta di masing-masing kotak.
-
Sifat 5: (a / b)n = an / bn
Ketika dua bilangan yang berbeda dibagi dan dipangkatkan, kekuatannya berlaku pada masing-masing bilangan. Misalnya, (2 / 3)2 = 22 / 32 = 4 / 9. Dalam kasus ini, pangkat 2 diterapkan pada kedua bilangan, 2 dan 3, secara terpisah. Ini seperti dua kunci yang membuka dua kotak yang berbeda, mengungkap harta di masing-masing kotak.
-
Sifat 6: a0 = 1
Ketika pangkatnya nol, kekuatannya menghilang. Misalnya, 20 = 1. Dalam kasus ini, pangkat 0 menghilangkan semua kekuatan yang ada. Ini seperti membuka kotak kosong, yang tidak memiliki harta di dalamnya.
-
Sifat 7: a-n = 1 / an
Ketika pangkatnya negatif, kekuatannya berbalik. Misalnya, 2-2 = 1 / 22 = 1 / 4. Dalam kasus ini, pangkat negatif, -2, mengubah kekuatan dari perkalian menjadi pembagian. Ini seperti kunci yang membuka kotak, tetapi bukan untuk mengambil harta, melainkan untuk meletakkan harta di dalamnya.
Penerapan Sifat-Sifat Pemangkatan Bilangan Berpangkat
Sifat-sifat pemangkatan bilangan berpangkat sangat berguna dalam menyelesaikan berbagai soal matematika, khususnya yang melibatkan bilangan berpangkat. Sifat-sifat ini membantu kita untuk menyederhanakan operasi pemangkatan, menemukan hasil yang tepat, dan memecahkan persamaan yang kompleks. Bayangkan, seperti detektif yang menggunakan petunjuk-petunjuk untuk mengungkap misteri, kita dapat menggunakan sifat-sifat ini untuk menemukan jawaban yang tersembunyi di balik operasi pemangkatan.
Cara Menentukan Hasil Pemangkatan Bilangan Berpangkat: Tentukan Hasil Pemangkatan Bilangan Berpangkat Berikut

Bayangkan kamu sedang menjelajahi sebuah labirin angka. Di setiap sudut, ada bilangan yang menjulang tinggi, dihiasi oleh angka-angka kecil yang menempel di atasnya. Angka-angka kecil ini seperti petunjuk rahasia, yang mengarahkanmu pada rahasia kekuatan tersembunyi dari bilangan besar itu. Nah, dalam dunia matematika, angka-angka kecil ini disebut “pangkat,” dan proses menemukan kekuatan tersembunyi mereka disebut “pemangkatan.” Siap untuk mengungkap misteri pemangkatan bilangan berpangkat? Mari kita mulai!
Langkah-Langkah Menentukan Hasil Pemangkatan Bilangan Berpangkat
Untuk mengungkap kekuatan tersembunyi dari bilangan berpangkat, kita perlu mengikuti serangkaian langkah yang terstruktur. Bayangkan ini seperti petunjuk rahasia untuk membuka kunci harta karun matematika. Berikut adalah langkah-langkahnya:
- Identifikasi Bilangan Pokok dan Pangkat: Bilangan pokok adalah bilangan yang akan dikalikan dengan dirinya sendiri, sedangkan pangkat menunjukkan berapa kali bilangan pokok dikalikan. Misalnya, dalam 23, 2 adalah bilangan pokok dan 3 adalah pangkat.
- Kalikan Bilangan Pokok Sesuai Pangkat: Kalikan bilangan pokok dengan dirinya sendiri sebanyak yang ditunjukkan oleh pangkat. Dalam contoh sebelumnya, 23 = 2 x 2 x 2 = 8.
Contoh Soal Pemangkatan Bilangan Berpangkat
Mari kita uji kemampuan kita dengan beberapa contoh soal. Siapkan dirimu, karena misteri pemangkatan akan segera terungkap!
- Contoh 1: Tentukan hasil dari 34.
- Penyelesaian: Bilangan pokok adalah 3 dan pangkatnya adalah 4. Jadi, 34 = 3 x 3 x 3 x 3 = 81.
- Contoh 2: Hitunglah hasil dari (-2)5.
- Penyelesaian: Bilangan pokok adalah -2 dan pangkatnya adalah 5. Karena pangkatnya ganjil, hasilnya akan bernilai negatif. Jadi, (-2)5 = (-2) x (-2) x (-2) x (-2) x (-2) = -32.
- Contoh 3: Tentukan hasil dari (1/2)3.
- Penyelesaian: Bilangan pokok adalah 1/2 dan pangkatnya adalah 3. Jadi, (1/2)3 = (1/2) x (1/2) x (1/2) = 1/8.
Flowchart Menentukan Hasil Pemangkatan Bilangan Berpangkat
Flowchart adalah diagram yang menggambarkan alur langkah-langkah dalam menyelesaikan suatu masalah. Bayangkan ini seperti peta yang menunjukkan jalan menuju solusi pemangkatan.
Gambar flowchart menunjukkan alur langkah-langkah menentukan hasil pemangkatan bilangan berpangkat.
Penerapan Pemangkatan Bilangan Berpangkat dalam Kehidupan Sehari-hari
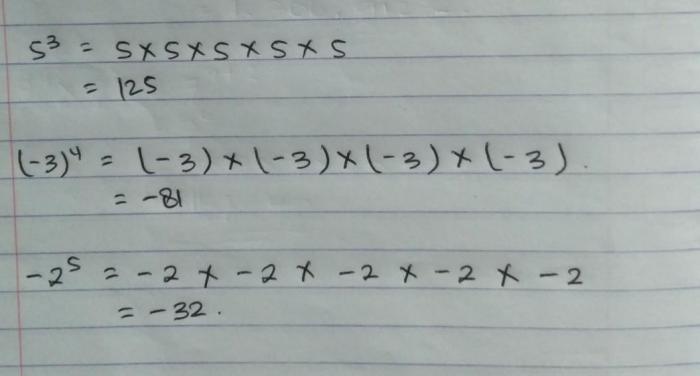
Pemangkatan bilangan berpangkat, sebuah konsep matematika yang mungkin terlihat rumit, ternyata memiliki peran penting dalam kehidupan kita sehari-hari. Dari menghitung jumlah bakteri yang berkembang biak hingga memahami bagaimana investasi kita tumbuh, pemangkatan berpangkat hadir di berbagai bidang, bahkan tanpa kita sadari.
Contoh Penerapan Pemangkatan Bilangan Berpangkat
Bayangkan sebuah bakteri yang mampu membelah diri menjadi dua setiap jam. Setelah satu jam, ada dua bakteri. Setelah dua jam, ada empat bakteri. Setelah tiga jam, ada delapan bakteri. Perhatikan pola yang muncul: 2, 4, 8, … Ini adalah contoh sederhana dari pertumbuhan eksponensial, yang diwakili oleh rumus 2n, di mana n adalah jumlah jam.
Contoh lainnya adalah menghitung jumlah kemungkinan kombinasi dari sebuah kunci. Jika sebuah kunci memiliki 10 tombol, setiap tombol memiliki 10 kemungkinan posisi. Untuk mendapatkan kombinasi kunci yang benar, kita perlu mencari tahu berapa banyak kemungkinan kombinasi yang ada. Rumus yang digunakan adalah 10n, di mana n adalah jumlah tombol pada kunci.
Penerapan Pemangkatan Bilangan Berpangkat dalam Bidang Keuangan
Dalam bidang keuangan, pemangkatan bilangan berpangkat digunakan untuk menghitung bunga majemuk. Bunga majemuk adalah bunga yang dihitung atas pokok pinjaman atau investasi ditambah dengan bunga yang telah terkumpul sebelumnya. Rumus yang digunakan adalah A = P(1 + r/n)nt, di mana A adalah jumlah akhir, P adalah pokok, r adalah suku bunga, n adalah jumlah kali bunga dihitung dalam setahun, dan t adalah waktu dalam tahun.
Contohnya, jika kita menginvestasikan Rp10.000.000,- dengan suku bunga 10% per tahun, dihitung setiap bulan, maka setelah 5 tahun, jumlah akhir kita akan menjadi Rp16.470.095,-. Ini adalah hasil dari penerapan rumus bunga majemuk, yang melibatkan pemangkatan bilangan berpangkat.
Tabel Contoh Penerapan Pemangkatan Bilangan Berpangkat
| Bidang | Contoh Penerapan | Rumus |
|---|---|---|
| Biologi | Pertumbuhan populasi bakteri | N = N0 * 2t |
| Fisika | Energi kinetik | Ek = 1/2 * m * v2 |
| Kimia | Konsentrasi larutan | C = n/V |
| Komputer | Jumlah kemungkinan kombinasi kunci | K = nm |