Pernahkah kamu memperhatikan bagaimana foto di handphone bisa diperbesar tanpa kehilangan detailnya? Atau bagaimana arsitek merancang bangunan yang proporsional dengan skala tertentu? Di balik keajaiban itu, terdapat konsep geometri yang menarik: kesebangunan. Rumus kesebangunan menjadi kunci untuk memahami hubungan antara dua bangun yang memiliki bentuk sama namun ukuran berbeda.
Kesebangunan bukan hanya teori abstrak, melainkan konsep yang diterapkan dalam berbagai bidang, mulai dari arsitektur dan desain hingga navigasi dan astronomi. Dalam artikel ini, kita akan menjelajahi dunia kesebangunan, mulai dari pengertian dasar hingga rumus-rumus yang mengendalikan hubungan antara bangun-bangun sebangun.
Pengertian Kesebangunan
Kesebangunan dalam geometri merupakan konsep yang menggambarkan hubungan antara dua bangun yang memiliki bentuk yang sama, namun ukurannya berbeda. Dua bangun dikatakan sebangun jika sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian sebanding.
Contoh Objek yang Sebangun
Contoh konkret objek yang sebangun adalah peta dan wilayah yang dipetakan. Peta merupakan representasi dari wilayah yang sebenarnya, namun dengan skala yang lebih kecil. Meskipun peta dan wilayah yang dipetakan memiliki bentuk yang sama, ukurannya berbeda. Hal ini menunjukkan bahwa peta dan wilayah yang dipetakan sebangun, karena sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian sebanding.
Perbandingan Sifat Bangun Datar Sebangun dan Tidak Sebangun
| Sifat | Bangun Datar Sebangun | Bangun Datar Tidak Sebangun |
|---|---|---|
| Sudut yang bersesuaian | Sama besar | Tidak sama besar |
| Sisi yang bersesuaian | Sebanding | Tidak sebanding |
| Bentuk | Sama | Berbeda |
| Ukuran | Berbeda | Berbeda |
Syarat Kesebangunan
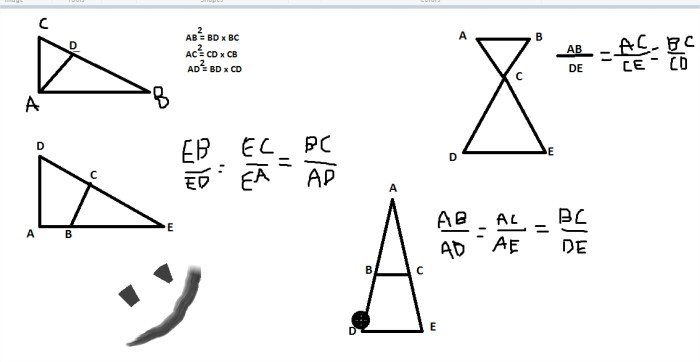
Dua bangun datar dikatakan sebangun jika memiliki bentuk yang sama tetapi ukurannya berbeda. Kesebangunan merupakan konsep penting dalam geometri yang membantu kita memahami hubungan antara bentuk dan ukuran. Dalam artikel ini, kita akan menjelajahi syarat-syarat yang harus dipenuhi agar dua bangun datar dapat dikatakan sebangun. Kita akan menggunakan ilustrasi gambar untuk membantu memahami konsep ini secara lebih jelas.
Syarat Kesebangunan
Agar dua bangun datar dapat dikatakan sebangun, mereka harus memenuhi tiga syarat utama:
- Sudut yang bersesuaian sama besar. Sudut yang bersesuaian adalah sudut yang memiliki posisi yang sama pada kedua bangun datar. Misalnya, jika dua bangun datar memiliki sudut A dan B, maka sudut A pada bangun pertama harus sama besar dengan sudut B pada bangun kedua.
- Sisi yang bersesuaian sebanding. Sisi yang bersesuaian adalah sisi yang memiliki posisi yang sama pada kedua bangun datar. Misalnya, jika dua bangun datar memiliki sisi AB dan CD, maka sisi AB pada bangun pertama harus sebanding dengan sisi CD pada bangun kedua. Artinya, perbandingan panjang sisi AB dan CD harus sama dengan perbandingan panjang sisi-sisi yang bersesuaian lainnya.
- Kedua bangun memiliki bentuk yang sama. Ini berarti bahwa kedua bangun datar memiliki sudut yang sama dan sisi yang sebanding, meskipun ukurannya berbeda.
Contoh Bangun Datar Tidak Sebangun
Misalnya, perhatikan dua segitiga berikut:
- Segitiga ABC dengan sudut A = 60 derajat, sudut B = 80 derajat, sudut C = 40 derajat, sisi AB = 5 cm, sisi BC = 6 cm, dan sisi AC = 7 cm.
- Segitiga DEF dengan sudut D = 60 derajat, sudut E = 80 derajat, sudut F = 40 derajat, sisi DE = 10 cm, sisi EF = 12 cm, dan sisi DF = 14 cm.
Kedua segitiga tersebut memiliki sudut yang sama besar, tetapi sisi-sisi yang bersesuaian tidak sebanding. Misalnya, perbandingan panjang sisi AB dan DE adalah 5:10, sedangkan perbandingan panjang sisi BC dan EF adalah 6:12. Perbandingan ini tidak sama, sehingga kedua segitiga tersebut tidak sebangun.
Jenis-jenis Kesebangunan: Rumus Kesebangunan
Dalam geometri, kesebangunan merupakan konsep penting yang menjelaskan hubungan antara dua bangun geometri yang memiliki bentuk sama namun ukuran yang berbeda. Dua bangun dikatakan sebangun jika semua sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian sebanding. Kesebangunan dapat dibedakan menjadi beberapa jenis, yang masing-masing memiliki karakteristik dan syarat yang berbeda.
Kesebangunan Berdasarkan Transformasi Geometri
Salah satu cara untuk memahami kesebangunan adalah dengan melihat transformasi geometri yang menghubungkan dua bangun sebangun. Transformasi geometri ini meliputi:
- Dilatasi: Dilatasi adalah transformasi yang mengubah ukuran bangun tanpa mengubah bentuknya. Dilatasi dapat memperbesar atau memperkecil bangun. Dua bangun yang sebangun melalui dilatasi memiliki perbandingan sisi yang sama.
- Translasi: Translasi adalah transformasi yang menggeser bangun tanpa mengubah ukuran atau bentuknya. Dua bangun yang sebangun melalui translasi memiliki bentuk dan ukuran yang sama, hanya saja posisinya berbeda.
- Rotasi: Rotasi adalah transformasi yang memutar bangun terhadap suatu titik tetap. Dua bangun yang sebangun melalui rotasi memiliki bentuk dan ukuran yang sama, hanya saja orientasinya berbeda.
- Refleksi: Refleksi adalah transformasi yang mencerminkan bangun terhadap suatu garis. Dua bangun yang sebangun melalui refleksi memiliki bentuk dan ukuran yang sama, hanya saja posisinya terbalik.
Perhatikan bahwa kesebangunan dapat terjadi melalui kombinasi beberapa transformasi geometri. Misalnya, dua bangun dapat sebangun melalui dilatasi dan translasi, atau melalui rotasi dan refleksi.
Kesebangunan Berdasarkan Sifat Sudut dan Sisi
Selain transformasi geometri, kesebangunan juga dapat didefinisikan berdasarkan sifat sudut dan sisi yang bersesuaian. Berikut adalah jenis-jenis kesebangunan berdasarkan sifat sudut dan sisi:
- Kesebangunan SSS (Side-Side-Side): Dua bangun dikatakan sebangun jika ketiga sisi yang bersesuaian sebanding. Contoh: Dua segitiga dengan panjang sisi 3 cm, 4 cm, dan 5 cm, dan segitiga lainnya dengan panjang sisi 6 cm, 8 cm, dan 10 cm, adalah sebangun karena perbandingan sisi-sisi yang bersesuaian adalah 1:2.
- Kesebangunan SAS (Side-Angle-Side): Dua bangun dikatakan sebangun jika dua sisi yang bersesuaian sebanding dan sudut yang diapit kedua sisi tersebut sama besar. Contoh: Dua segitiga dengan panjang sisi 3 cm, 4 cm, dan sudut 60 derajat, dan segitiga lainnya dengan panjang sisi 6 cm, 8 cm, dan sudut 60 derajat, adalah sebangun karena dua sisi yang bersesuaian sebanding (1:2) dan sudut yang diapit kedua sisi tersebut sama besar (60 derajat).
- Kesebangunan ASA (Angle-Side-Angle): Dua bangun dikatakan sebangun jika dua sudut yang bersesuaian sama besar dan sisi yang diapit kedua sudut tersebut sebanding. Contoh: Dua segitiga dengan sudut 45 derajat, 60 derajat, dan panjang sisi 5 cm yang diapit kedua sudut tersebut, dan segitiga lainnya dengan sudut 45 derajat, 60 derajat, dan panjang sisi 10 cm yang diapit kedua sudut tersebut, adalah sebangun karena dua sudut yang bersesuaian sama besar (45 derajat dan 60 derajat) dan sisi yang diapit kedua sudut tersebut sebanding (1:2).
- Kesebangunan AA (Angle-Angle): Dua bangun dikatakan sebangun jika dua sudut yang bersesuaian sama besar. Contoh: Dua segitiga dengan sudut 30 derajat, 60 derajat, dan sudut 90 derajat, dan segitiga lainnya dengan sudut 30 derajat, 60 derajat, dan sudut 90 derajat, adalah sebangun karena dua sudut yang bersesuaian sama besar.
Tabel Jenis-jenis Kesebangunan, Rumus kesebangunan
| Jenis Kesebangunan | Syarat | Contoh |
|---|---|---|
| SSS (Side-Side-Side) | Ketiga sisi yang bersesuaian sebanding | Dua segitiga dengan panjang sisi 3 cm, 4 cm, dan 5 cm, dan segitiga lainnya dengan panjang sisi 6 cm, 8 cm, dan 10 cm |
| SAS (Side-Angle-Side) | Dua sisi yang bersesuaian sebanding dan sudut yang diapit kedua sisi tersebut sama besar | Dua segitiga dengan panjang sisi 3 cm, 4 cm, dan sudut 60 derajat, dan segitiga lainnya dengan panjang sisi 6 cm, 8 cm, dan sudut 60 derajat |
| ASA (Angle-Side-Angle) | Dua sudut yang bersesuaian sama besar dan sisi yang diapit kedua sudut tersebut sebanding | Dua segitiga dengan sudut 45 derajat, 60 derajat, dan panjang sisi 5 cm yang diapit kedua sudut tersebut, dan segitiga lainnya dengan sudut 45 derajat, 60 derajat, dan panjang sisi 10 cm yang diapit kedua sudut tersebut |
| AA (Angle-Angle) | Dua sudut yang bersesuaian sama besar | Dua segitiga dengan sudut 30 derajat, 60 derajat, dan sudut 90 derajat, dan segitiga lainnya dengan sudut 30 derajat, 60 derajat, dan sudut 90 derajat |
Penerapan Kesebangunan dalam Kehidupan Sehari-hari
Konsep kesebangunan tidak hanya terbatas pada ruang lingkup matematika. Dalam kehidupan sehari-hari, prinsip kesebangunan bekerja secara diam-diam, membantu kita dalam berbagai aktivitas dan pekerjaan. Mari kita bahas beberapa contoh konkret penerapan kesebangunan dalam kehidupan sehari-hari.
Pembuatan Peta dan Denah
Salah satu aplikasi paling umum dari kesebangunan adalah dalam pembuatan peta dan denah. Peta dan denah merupakan representasi visual dari area yang lebih besar, namun dengan skala yang lebih kecil. Prinsip kesebangunan memastikan bahwa semua proporsi dan jarak dalam peta atau denah tetap terjaga, sehingga kita dapat memahami tata letak dan jarak sebenarnya dari suatu area.
- Misalnya, peta kota menunjukkan jalan, bangunan, dan sungai dengan proporsi yang sesuai dengan ukuran sebenarnya.
- Sebuah denah rumah menunjukkan tata letak ruangan, ukuran, dan jarak antar ruangan dengan skala yang tepat.
Dalam kedua contoh tersebut, kesebangunan memastikan bahwa semua elemen dalam peta atau denah memiliki proporsi yang tepat dengan objek aslinya. Ini memungkinkan kita untuk menavigasi dan memahami tata letak area tersebut dengan mudah.
Fotografi
Kesebangunan juga memainkan peran penting dalam fotografi. Saat mengambil gambar, kamera menangkap gambar tiga dimensi dan mengubahnya menjadi gambar dua dimensi. Proses ini memanfaatkan prinsip kesebangunan untuk mempertahankan proporsi dan bentuk objek dalam gambar.
- Misalnya, ketika mengambil gambar bangunan, kamera menangkap semua sisi bangunan dengan proporsi yang benar, sehingga gambar yang dihasilkan tetap mempertahankan bentuk dan ukuran aslinya.
- Begitu pula ketika mengambil gambar objek kecil, seperti serangga, kamera dapat memperbesar objek tersebut tanpa mengubah bentuk dan proporsi aslinya.
Kesebangunan dalam fotografi memungkinkan kita untuk merekam dan melihat dunia dengan cara yang akurat, dan membantu kita untuk mengabadikan momen dan objek dengan detail yang tepat.
Arsitektur
Arsitektur adalah bidang lain yang mengandalkan konsep kesebangunan. Arsitek menggunakan prinsip kesebangunan untuk mendesain bangunan dengan proporsi yang harmonis dan estetis.
- Contohnya, dalam desain bangunan dengan bentuk simetris, arsitek menggunakan prinsip kesebangunan untuk memastikan bahwa kedua sisi bangunan memiliki proporsi yang sama.
- Kesebangunan juga digunakan dalam mendesain jendela, pintu, dan elemen arsitektur lainnya untuk memastikan bahwa mereka memiliki proporsi yang tepat dan seimbang dengan keseluruhan desain bangunan.
Dengan menggunakan prinsip kesebangunan, arsitek dapat menciptakan bangunan yang indah, fungsional, dan harmonis.
Seni Rupa
Konsep kesebangunan juga dapat diterapkan dalam seni rupa, khususnya dalam lukisan dan seni grafis. Seniman menggunakan prinsip kesebangunan untuk menciptakan komposisi yang seimbang dan harmonis dalam karya seni mereka.
- Contohnya, dalam lukisan lanskap, seniman dapat menggunakan kesebangunan untuk menggambarkan proporsi yang tepat dari gunung, pohon, dan sungai dalam lanskap tersebut.
- Dalam seni grafis, prinsip kesebangunan digunakan untuk menciptakan desain yang seimbang dan harmonis, seperti logo dan ilustrasi.
Dengan memahami dan menerapkan prinsip kesebangunan, seniman dapat menciptakan karya seni yang estetis dan menarik.
Rumus Kesebangunan
Kesebangunan merupakan konsep penting dalam geometri yang mengkaji hubungan antara dua bangun datar yang memiliki bentuk sama namun ukuran yang berbeda. Dalam kesebangunan, dua bangun dikatakan sebangun jika semua sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian sebanding. Untuk menentukan kesebangunan dua bangun datar, kita dapat menggunakan rumus-rumus tertentu yang akan kita bahas lebih lanjut.
Rumus Kesebangunan
Rumus-rumus kesebangunan digunakan untuk menghitung panjang sisi atau sudut pada bangun datar sebangun. Rumus-rumus ini didasarkan pada konsep perbandingan sisi dan sudut yang bersesuaian. Berikut adalah beberapa rumus penting yang berkaitan dengan kesebangunan:
- Perbandingan Sisi: Jika dua bangun datar sebangun, maka perbandingan sisi-sisi yang bersesuaian selalu sama. Misalnya, jika sisi-sisi segitiga ABC sebanding dengan sisi-sisi segitiga DEF, maka berlaku:
- AB/DE = BC/EF = AC/DF
- Perbandingan Sudut: Jika dua bangun datar sebangun, maka sudut-sudut yang bersesuaian sama besar. Misalnya, jika sudut A pada segitiga ABC bersesuaian dengan sudut D pada segitiga DEF, maka berlaku:
- ∠A = ∠D
Cara Menggunakan Rumus Kesebangunan
Rumus-rumus kesebangunan dapat digunakan untuk menghitung panjang sisi atau sudut pada bangun datar sebangun. Misalnya, jika kita mengetahui panjang dua sisi dari sebuah segitiga dan panjang sisi yang bersesuaian pada segitiga sebangunnya, maka kita dapat menghitung panjang sisi lainnya pada segitiga sebangun tersebut.
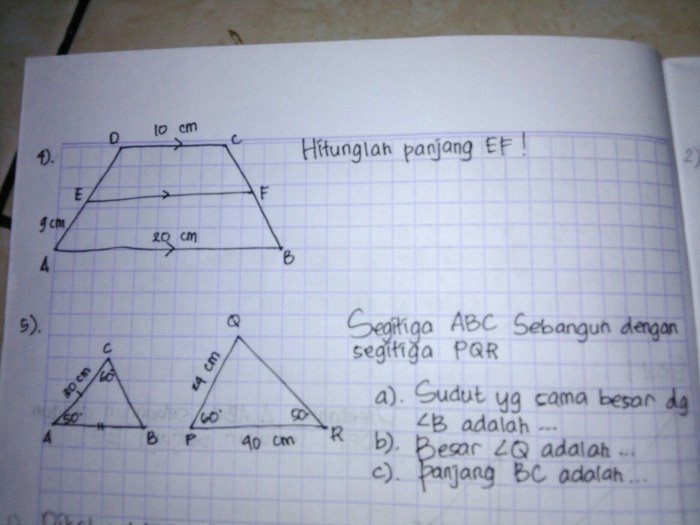
Sebagai contoh, perhatikan segitiga ABC dan segitiga DEF di bawah ini:
Jika diketahui bahwa AB = 6 cm, BC = 8 cm, dan DE = 3 cm, maka kita dapat menghitung panjang EF dengan menggunakan rumus perbandingan sisi:
- AB/DE = BC/EF
- 6/3 = 8/EF
- EF = 4 cm
Dengan demikian, panjang EF adalah 4 cm.
Contoh Soal
Sebuah persegi panjang ABCD memiliki panjang 12 cm dan lebar 8 cm. Persegi panjang EFGH sebangun dengan ABCD dan memiliki panjang 6 cm. Hitunglah lebar persegi panjang EFGH.
Penyelesaian:
- Pertama, kita ketahui bahwa ABCD dan EFGH sebangun. Ini berarti bahwa perbandingan sisi-sisi yang bersesuaian selalu sama.
- Kita juga tahu bahwa panjang ABCD adalah 12 cm dan panjang EFGH adalah 6 cm. Oleh karena itu, perbandingan panjang ABCD dan EFGH adalah 12/6 = 2.
- Karena perbandingan sisi-sisi yang bersesuaian sama, maka perbandingan lebar ABCD dan EFGH juga sama dengan 2.
- Lebar ABCD adalah 8 cm, maka lebar EFGH adalah 8/2 = 4 cm.
Jadi, lebar persegi panjang EFGH adalah 4 cm.












