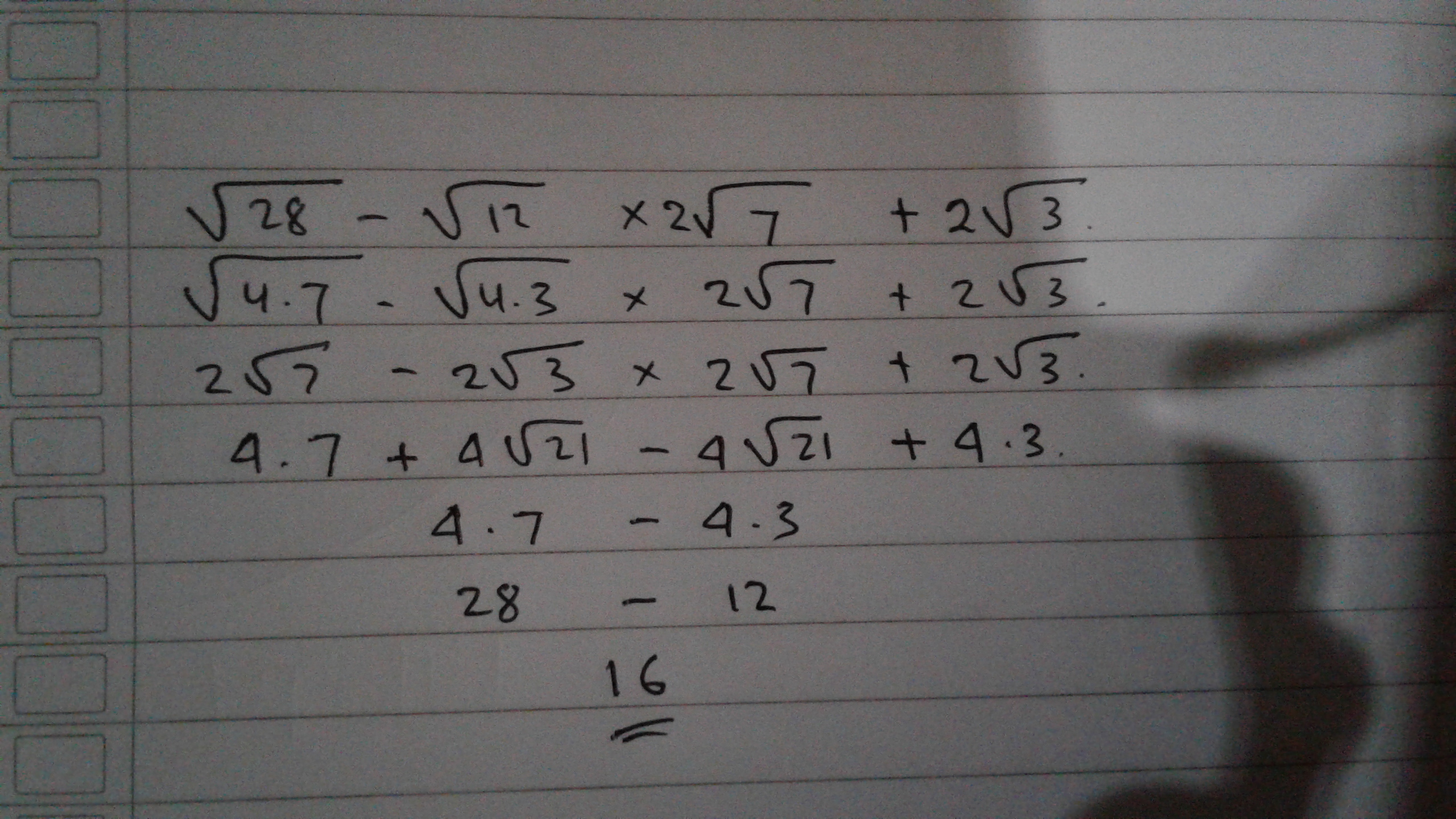Yo, bro! Pernah ngebayangin, gimana sih hasil dari akar 2 dikali akar 2? Kayak gini, bro, akar 2 itu kan bilangan irasional, jadi kayak ngitung sesuatu yang nggak kelihatan bentuknya. Tapi, tenang aja, kita bakal ngebongkar misteri ini bareng-bareng. Akar 2 dikali akar 2 itu ternyata punya hasil yang super simple dan penting banget dalam dunia matematika.
Nah, buat ngerti konsep ini, kita bakal bahas tentang akar kuadrat, sifat-sifatnya, dan gimana cara ngitungnya. Kalian juga bakal tau, kenapa akar 2 dikali akar 2 penting banget buat ngerjain soal-soal matematika, khususnya di geometri. So, siap-siap buat ngelacak jawabannya, bro!
Akar Kuadrat: Sebuah Konsep Dasar dalam Matematika: Akar 2 Dikali Akar 2
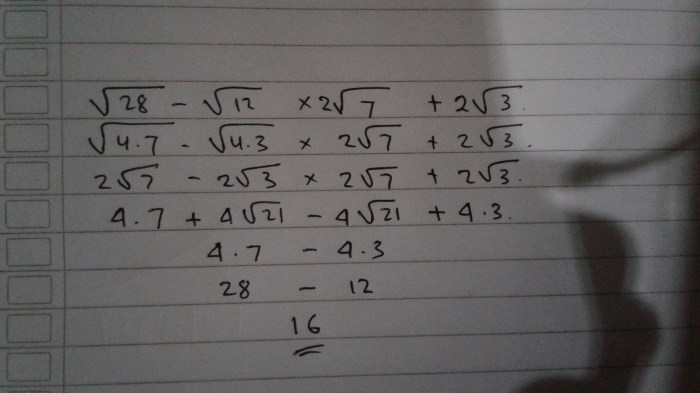
Akar kuadrat adalah konsep fundamental dalam matematika yang memiliki aplikasi luas di berbagai bidang, mulai dari geometri hingga fisika. Secara sederhana, akar kuadrat dari suatu bilangan adalah bilangan yang, jika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli tersebut. Konsep ini penting karena memungkinkan kita untuk menemukan panjang sisi segitiga siku-siku, memecahkan persamaan kuadrat, dan memahami berbagai fenomena matematis lainnya.
Pengertian Akar Kuadrat
Akar kuadrat dari suatu bilangan adalah bilangan yang, jika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli tersebut. Dengan kata lain, akar kuadrat adalah kebalikan dari operasi kuadrat. Simbol yang digunakan untuk mewakili akar kuadrat adalah tanda akar, √. Misalnya, akar kuadrat dari 9 adalah 3, karena 3 x 3 = 9. Kita menulis ini sebagai √9 = 3.
Contoh Perhitungan Akar Kuadrat
Berikut beberapa contoh perhitungan akar kuadrat:
- √4 = 2, karena 2 x 2 = 4
- √16 = 4, karena 4 x 4 = 16
- √25 = 5, karena 5 x 5 = 25
Hubungan antara Bilangan, Kuadratnya, dan Akar Kuadratnya
Berikut tabel yang menunjukkan hubungan antara bilangan, kuadratnya, dan akar kuadratnya:
| Bilangan | Kuadrat | Akar Kuadrat |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 4 | 2 |
| 3 | 9 | 3 |
| 4 | 16 | 4 |
| 5 | 25 | 5 |
Sifat Akar Kuadrat
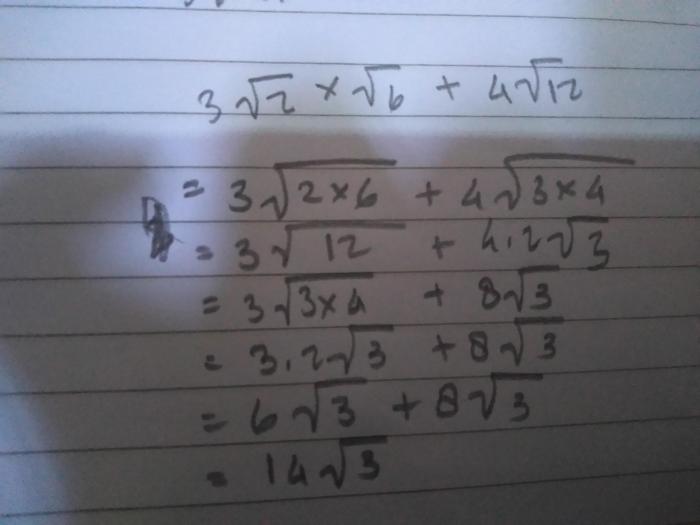
Akar kuadrat adalah operasi matematika yang mencari bilangan yang, jika dikalikan dengan dirinya sendiri, menghasilkan bilangan asli. Sifat perkalian akar kuadrat memberikan kita cara mudah untuk menghitung hasil perkalian dua akar kuadrat.
Sifat Perkalian Akar Kuadrat
Sifat perkalian akar kuadrat menyatakan bahwa perkalian dua akar kuadrat sama dengan akar kuadrat dari hasil kali kedua bilangan tersebut. Secara matematis, sifat ini dapat ditulis sebagai:
√a x √b = √(a x b)
Dengan kata lain, untuk mengalikan dua akar kuadrat, kita dapat mengalikan bilangan di bawah tanda akar dan kemudian mengambil akar kuadrat dari hasil kali tersebut.
Contoh Perhitungan √2 x √2
Mari kita terapkan sifat perkalian akar kuadrat untuk menghitung √2 x √2.
- Berdasarkan sifat perkalian akar kuadrat, √2 x √2 = √(2 x 2).
- Hasil kali 2 x 2 adalah 4, sehingga √2 x √2 = √4.
- Akar kuadrat dari 4 adalah 2, karena 2 x 2 = 4. Jadi, √2 x √2 = 2.
Langkah-langkah Menghitung √2 x √2 dengan Kalkulator
Berikut adalah langkah-langkah untuk menghitung √2 x √2 menggunakan kalkulator:
- Tekan tombol “√” (akar kuadrat) pada kalkulator.
- Masukkan angka 2.
- Tekan tombol “x” (perkalian).
- Tekan tombol “√” (akar kuadrat) lagi.
- Masukkan angka 2.
- Tekan tombol “=” (sama dengan).
- Hasilnya akan ditampilkan sebagai 2.
Pembahasan Lebih Lanjut
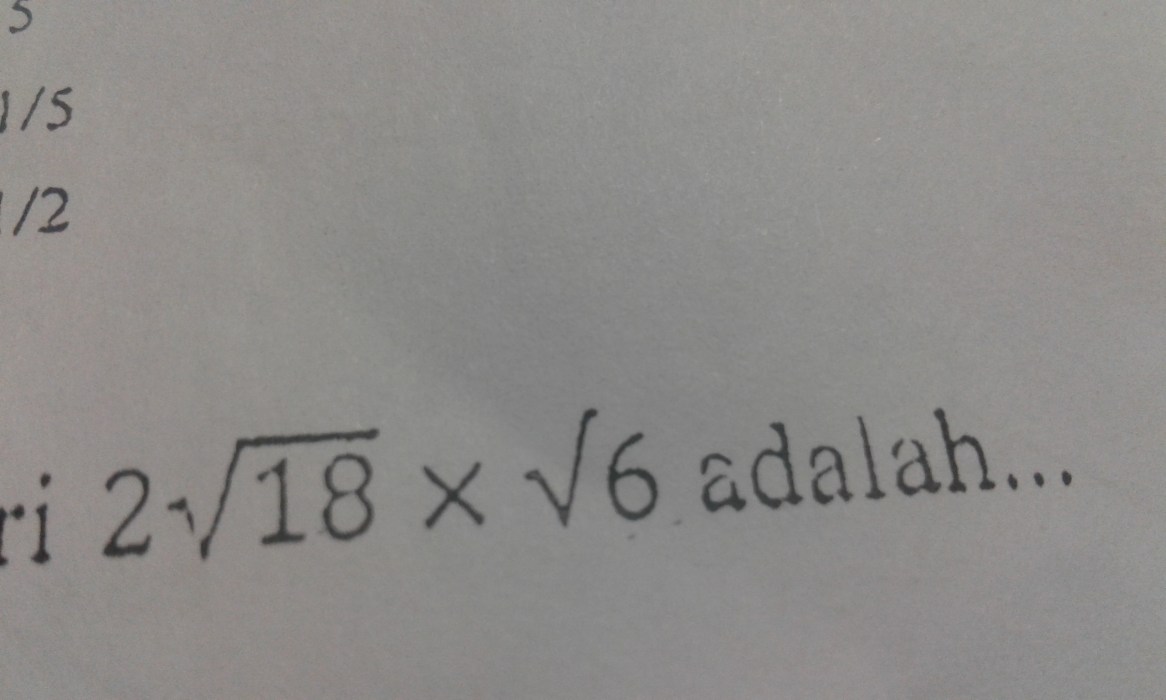
Sekarang, mari kita selami lebih dalam tentang akar kuadrat dan hubungannya dengan bilangan rasional dan irasional. Kita akan menjelajahi bagaimana akar kuadrat memainkan peran penting dalam menyelesaikan persamaan kuadrat. Perjalanan ini akan mengungkap rahasia yang tersembunyi di balik konsep-konsep matematika ini.
Hubungan Akar Kuadrat dengan Bilangan Rasional dan Irasional
Akar kuadrat, yang merupakan operasi matematika yang menghasilkan bilangan yang dikalikan dengan dirinya sendiri untuk menghasilkan bilangan awal, memiliki hubungan erat dengan bilangan rasional dan irasional. Bilangan rasional dapat ditulis sebagai pecahan dari dua bilangan bulat, sementara bilangan irasional tidak dapat dinyatakan sebagai pecahan sederhana.
- Akar kuadrat dari bilangan bulat sempurna adalah bilangan rasional. Misalnya, akar kuadrat dari 9 adalah 3, yang merupakan bilangan bulat dan juga dapat ditulis sebagai pecahan 3/1.
- Akar kuadrat dari bilangan bulat yang bukan sempurna adalah bilangan irasional. Sebagai contoh, akar kuadrat dari 2, yang kita telah bahas sebelumnya, adalah bilangan irasional. Tidak mungkin untuk menulis akar kuadrat dari 2 sebagai pecahan sederhana.
Penggunaan Akar Kuadrat dalam Menyelesaikan Persamaan Kuadrat, Akar 2 dikali akar 2
Akar kuadrat memainkan peran penting dalam menyelesaikan persamaan kuadrat, yang merupakan persamaan yang melibatkan variabel pangkat dua. Persamaan kuadrat umumnya ditulis dalam bentuk ax² + bx + c = 0, di mana a, b, dan c adalah konstanta. Untuk menemukan solusi untuk persamaan ini, kita dapat menggunakan rumus kuadrat, yang melibatkan penggunaan akar kuadrat.
Rumus kuadrat: x = (-b ± √(b² – 4ac)) / 2a
Rumus ini memberi kita dua solusi yang mungkin untuk persamaan kuadrat, yang dapat berupa bilangan rasional atau irasional, tergantung pada nilai diskriminan (b² – 4ac).
Ilustrasi Perbedaan Bilangan Rasional dan Irasional
Bayangkan sebuah garis bilangan. Bilangan rasional menempati posisi tertentu pada garis ini, seperti 1, 2, 3, atau 1/2, 3/4, dan seterusnya. Namun, bilangan irasional seperti akar kuadrat dari 2 tidak memiliki posisi yang pasti pada garis bilangan ini. Mereka berada di antara bilangan rasional, seperti titik-titik di antara titik-titik pada garis.
| Bilangan | Jenis | Representasi |
|---|---|---|
| 2 | Rasional | 2/1 |
| √4 | Rasional | 2/1 |
| √2 | Irasional | Tidak dapat dinyatakan sebagai pecahan sederhana |
Ilustrasi ini menunjukkan bahwa bilangan irasional seperti akar kuadrat dari 2 memiliki sifat unik yang membedakannya dari bilangan rasional.