Mencari Nilai Minimum Fungsi Objektif: Kunci Optimasi dan Pengambilan Keputusan

Bayangkan Anda sedang merencanakan perjalanan liburan yang sempurna. Anda ingin mengunjungi sebanyak mungkin tempat wisata dengan biaya seminimal mungkin. Atau, bayangkan Anda adalah seorang pengusaha yang ingin memaksimalkan keuntungan dengan meminimalkan biaya produksi. Dalam kedua skenario ini, Anda menghadapi sebuah tantangan: menemukan nilai minimum dari fungsi objektif. Fungsi objektif ini merepresentasikan tujuan yang ingin Anda capai, seperti meminimalkan biaya atau memaksimalkan keuntungan. Nilai minimum fungsi objektif menjadi kunci untuk mencapai tujuan tersebut secara optimal.

Konsep nilai minimum fungsi objektif memainkan peran penting dalam berbagai bidang, mulai dari ekonomi dan bisnis hingga ilmu komputer dan rekayasa. Dalam optimasi, tujuannya adalah untuk menemukan nilai input yang menghasilkan output minimum dari fungsi objektif. Hal ini dapat diartikan sebagai mencari titik terendah dari kurva fungsi. Nilai minimum ini menjadi titik acuan dalam pengambilan keputusan, membantu kita untuk memilih strategi terbaik untuk mencapai hasil yang optimal.

Daftar Isi:

Pengertian Nilai Minimum Fungsi Objektif

Dalam dunia optimasi, nilai minimum fungsi objektif merupakan titik fokus utama. Fungsi objektif sendiri adalah persamaan matematika yang menggambarkan target yang ingin dicapai dalam suatu proses optimasi. Target tersebut dapat berupa meminimalkan biaya, memaksimalkan keuntungan, atau mencapai efisiensi terbaik. Nilai minimum fungsi objektif merepresentasikan titik terendah yang dapat dicapai oleh fungsi tersebut, yang berarti mencapai hasil optimal sesuai dengan tujuan yang telah ditetapkan.

Contoh Penerapan Nilai Minimum Fungsi Objektif

Bayangkan sebuah perusahaan manufaktur yang ingin meminimalkan biaya produksi. Mereka dapat menggunakan fungsi objektif untuk menggambarkan total biaya produksi sebagai fungsi dari jumlah unit yang diproduksi, bahan baku, dan biaya tenaga kerja. Nilai minimum fungsi objektif dalam kasus ini akan menunjukkan jumlah unit yang harus diproduksi, bahan baku yang digunakan, dan tenaga kerja yang dibutuhkan untuk mencapai biaya produksi terendah.

Perbedaan Nilai Minimum dan Maksimum Fungsi Objektif

Aspek	Nilai Minimum Fungsi Objektif	Nilai Maksimum Fungsi Objektif
Tujuan	Mencari titik terendah dari fungsi objektif	Mencari titik tertinggi dari fungsi objektif
Contoh Aplikasi	Meminimalkan biaya produksi, meminimalkan waktu pengiriman, meminimalkan risiko	Memaksimalkan keuntungan, memaksimalkan efisiensi, memaksimalkan hasil produksi
Contoh dalam Kehidupan Sehari-hari	Mencari rute terpendek untuk bepergian, memilih bahan bangunan dengan harga terendah	Memilih investasi dengan potensi keuntungan tertinggi, memilih produk dengan kualitas terbaik

Metode Pencarian Nilai Minimum Fungsi Objektif

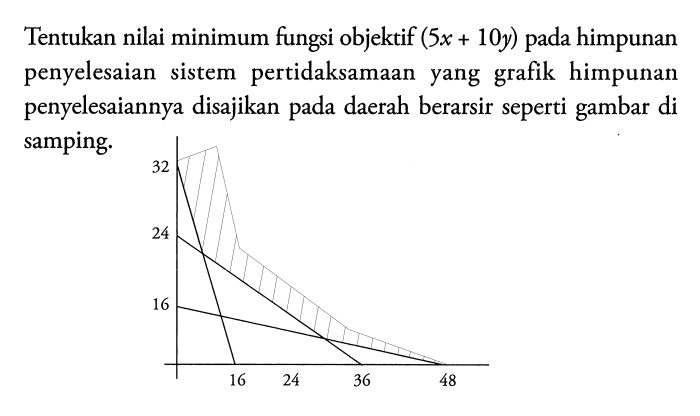
Menentukan nilai minimum dari suatu fungsi objektif merupakan langkah krusial dalam berbagai bidang, seperti optimasi, ekonomi, dan ilmu komputer. Fungsi objektif merepresentasikan tujuan yang ingin dicapai, dan nilai minimumnya menunjukkan solusi optimal untuk mencapai tujuan tersebut. Dalam konteks ini, metode pencarian nilai minimum fungsi objektif menjadi sangat penting untuk menemukan solusi optimal yang diinginkan.

Langkah-Langkah Umum dalam Mencari Nilai Minimum Fungsi Objektif

Proses pencarian nilai minimum fungsi objektif umumnya melibatkan beberapa langkah penting, yaitu:

Mendefinisikan Fungsi Objektif: Langkah pertama adalah mendefinisikan fungsi objektif yang ingin diminimalkan. Fungsi ini biasanya merupakan persamaan matematika yang menggambarkan hubungan antara variabel-variabel yang terlibat dan tujuan yang ingin dicapai.
Menentukan Batasan atau Kendala: Fungsi objektif seringkali memiliki batasan atau kendala yang harus dipenuhi. Batasan ini dapat berupa persamaan atau pertidaksamaan yang membatasi nilai variabel-variabel yang dapat diterima.
Memilih Metode Pencarian: Berbagai metode pencarian dapat digunakan untuk menemukan nilai minimum fungsi objektif. Beberapa metode yang umum digunakan adalah:

Metode Gradien Turun: Metode ini menggunakan gradien fungsi objektif untuk menentukan arah penurunan yang paling curam menuju nilai minimum.
Metode Newton-Raphson: Metode ini menggunakan turunan kedua fungsi objektif untuk memperkirakan nilai minimum dengan lebih cepat.
Metode Simplex: Metode ini digunakan untuk menyelesaikan masalah optimasi linier, di mana fungsi objektif dan batasannya adalah fungsi linier.

Melakukan Iterasi: Setelah memilih metode pencarian, proses pencarian nilai minimum dilakukan secara iteratif. Pada setiap iterasi, nilai variabel-variabel diubah berdasarkan metode yang dipilih, dan nilai fungsi objektif dihitung.
Menghentikan Iterasi: Iterasi dihentikan ketika mencapai kriteria penghentian, misalnya ketika perubahan nilai fungsi objektif sangat kecil atau ketika mencapai batas iterasi maksimum.
Menetapkan Nilai Minimum: Setelah iterasi dihentikan, nilai variabel-variabel yang menghasilkan nilai fungsi objektif terkecil dianggap sebagai nilai minimum.

Contoh Penerapan Metode Pencarian Nilai Minimum Fungsi Objektif dalam Bidang Manajemen Operasional

Salah satu contoh penerapan metode pencarian nilai minimum fungsi objektif adalah dalam masalah optimasi produksi. Sebuah perusahaan manufaktur ingin memaksimalkan keuntungannya dengan menentukan jumlah produk yang optimal untuk diproduksi. Fungsi objektif dalam kasus ini adalah fungsi keuntungan, yang merupakan selisih antara pendapatan dan biaya produksi. Batasannya adalah ketersediaan sumber daya, seperti bahan baku, tenaga kerja, dan kapasitas produksi.

Dengan menggunakan metode pencarian nilai minimum fungsi objektif, perusahaan dapat menemukan jumlah produk yang optimal untuk diproduksi yang memaksimalkan keuntungannya. Dalam hal ini, metode Simplex dapat digunakan untuk menyelesaikan masalah optimasi linier yang terkait dengan fungsi keuntungan dan batasan sumber daya.

Demonstrasi Penggunaan Algoritma Pencarian Nilai Minimum Fungsi Objektif melalui Contoh Sederhana

Perhatikan fungsi objektif berikut:

f(x) = x² – 4x + 3

Tujuannya adalah untuk menemukan nilai minimum dari fungsi ini. Untuk demonstrasi ini, kita akan menggunakan metode gradien turun. Langkah-langkahnya adalah sebagai berikut:

Menentukan Turunan Pertama: Turunan pertama fungsi f(x) adalah f'(x) = 2x – 4.
Menentukan Nilai Awal: Kita akan mulai dengan nilai awal x = 2.
Melakukan Iterasi: Pada setiap iterasi, nilai x diperbarui dengan menggunakan rumus berikut:

x_n+1 = x_n – αf'(x_n)

di mana α adalah learning rate yang menentukan ukuran langkah pada setiap iterasi. Dalam contoh ini, kita akan menggunakan α = 0.1.

Menerapkan Rumus: Iterasi pertama:

x₁ = x₀ – αf'(x₀) = 2 – 0.1(2(2) – 4) = 2

Iterasi kedua:

x₂ = x₁ – αf'(x₁) = 2 – 0.1(2(2) – 4) = 2

Iterasi ketiga:

x₃ = x₂ – αf'(x₂) = 2 – 0.1(2(2) – 4) = 2

Dalam contoh ini, nilai x tidak berubah setelah iterasi pertama. Ini menunjukkan bahwa nilai minimum fungsi f(x) adalah x = 2.

Menghitung Nilai Minimum: Dengan x = 2, nilai minimum fungsi f(x) adalah:

f(2) = 2² – 4(2) + 3 = -1

Oleh karena itu, nilai minimum fungsi objektif f(x) = x² – 4x + 3 adalah -1, yang terjadi pada x = 2.

Penerapan Nilai Minimum Fungsi Objektif

Nilai minimum fungsi objektif merupakan titik kunci dalam berbagai bidang, terutama dalam pengambilan keputusan. Dalam dunia bisnis, ekonomi, dan ilmu komputer, meminimalkan fungsi objektif berarti menemukan solusi terbaik untuk mencapai tujuan tertentu, seperti memaksimalkan keuntungan, meminimalkan biaya, atau mengoptimalkan kinerja sistem.

Penerapan Nilai Minimum Fungsi Objektif dalam Berbagai Bidang

Penerapan nilai minimum fungsi objektif sangat luas dan memiliki peran penting dalam berbagai bidang, seperti:

Ekonomi: Dalam ekonomi, nilai minimum fungsi objektif dapat diterapkan untuk meminimalkan biaya produksi, memaksimalkan keuntungan, atau menemukan titik keseimbangan pasar. Misalnya, perusahaan dapat menggunakan pemrograman linier untuk menentukan jumlah produk yang optimal untuk diproduksi agar dapat memaksimalkan keuntungan, dengan mempertimbangkan kendala seperti biaya produksi dan ketersediaan bahan baku.
Bisnis: Dalam bisnis, nilai minimum fungsi objektif dapat digunakan untuk mengoptimalkan berbagai proses, seperti manajemen inventaris, perencanaan produksi, dan strategi pemasaran. Misalnya, perusahaan ritel dapat menggunakan algoritma optimasi untuk menentukan jumlah produk yang optimal untuk disimpan di gudang, dengan mempertimbangkan biaya penyimpanan dan permintaan pasar.
Ilmu Komputer: Dalam ilmu komputer, nilai minimum fungsi objektif dapat diterapkan dalam berbagai bidang, seperti kecerdasan buatan, pembelajaran mesin, dan pengolahan citra. Misalnya, algoritma pembelajaran mesin dapat menggunakan fungsi objektif untuk menemukan model yang paling akurat untuk memprediksi hasil, dengan mempertimbangkan data pelatihan dan kriteria evaluasi.

Ilustrasi Pengaruh Nilai Minimum Fungsi Objektif

Bayangkan sebuah perusahaan yang memproduksi sepatu. Fungsi objektifnya adalah meminimalkan biaya produksi, dengan kendala berupa ketersediaan bahan baku, kapasitas produksi, dan permintaan pasar.

Dengan menggunakan metode optimasi, perusahaan dapat menemukan nilai minimum fungsi objektif, yang berarti kombinasi terbaik dari bahan baku, kapasitas produksi, dan harga jual yang menghasilkan biaya produksi terendah.

Ilustrasi ini menunjukkan bagaimana nilai minimum fungsi objektif dapat membantu perusahaan untuk membuat keputusan yang optimal, dalam hal ini, meminimalkan biaya produksi dan meningkatkan profitabilitas.

Keterbatasan dan Tantangan dalam Pencarian Nilai Minimum Fungsi Objektif

Pencarian nilai minimum fungsi objektif merupakan proses yang fundamental dalam berbagai bidang, seperti optimasi, ilmu komputer, dan ekonomi. Namun, proses ini tidak selalu mudah dan seringkali dihadapkan pada keterbatasan dan tantangan yang perlu diatasi.

Keterbatasan dalam Pencarian Nilai Minimum Fungsi Objektif

Keterbatasan dalam mencari nilai minimum fungsi objektif dapat muncul dari berbagai aspek, termasuk:

Kompleksitas Fungsi Objektif: Fungsi objektif yang rumit dengan banyak variabel dan persamaan dapat menyulitkan proses pencarian nilai minimum. Algoritma optimasi yang sederhana mungkin tidak efektif dalam menangani kompleksitas ini.
Ketidakberaturan Fungsi: Fungsi objektif yang tidak beraturan, seperti fungsi dengan banyak titik minimum lokal, dapat membuat pencarian nilai minimum menjadi menantang. Algoritma optimasi dapat terjebak dalam titik minimum lokal, tanpa mencapai nilai minimum global.
Keterbatasan Data: Kurangnya data yang cukup atau data yang tidak akurat dapat memengaruhi ketepatan pencarian nilai minimum. Model yang dibangun berdasarkan data yang tidak lengkap atau tidak akurat mungkin tidak mencerminkan realitas dengan baik.
Keterbatasan Komputasi: Fungsi objektif yang sangat kompleks dapat memerlukan waktu komputasi yang lama untuk menemukan nilai minimum. Keterbatasan daya komputasi dapat menjadi hambatan dalam proses optimasi.

Tantangan dalam Menentukan Nilai Minimum Fungsi Objektif

Menentukan nilai minimum fungsi objektif dalam kasus-kasus tertentu dapat dihadapkan pada tantangan yang signifikan. Beberapa contohnya adalah:

Fungsi Non-Konveks: Fungsi non-konveks memiliki banyak titik minimum lokal, yang menyulitkan pencarian nilai minimum global. Algoritma optimasi yang dirancang untuk fungsi konveks mungkin tidak efektif dalam menangani fungsi non-konveks.
Keterbatasan Batas: Batas atau kendala yang diterapkan pada variabel fungsi objektif dapat memperumit proses pencarian nilai minimum. Algoritma optimasi harus mempertimbangkan batasan ini dalam pencarian solusi.
Fungsi Multi-Objektif: Fungsi multi-objektif melibatkan lebih dari satu fungsi objektif yang harus dioptimalkan secara bersamaan. Menemukan solusi yang optimal untuk semua fungsi objektif secara bersamaan bisa menjadi tantangan yang besar.

Pertanyaan untuk Diskusi Lebih Lanjut

Berikut adalah beberapa pertanyaan yang dapat memicu diskusi lebih lanjut tentang keterbatasan dan tantangan dalam pencarian nilai minimum fungsi objektif:

Bagaimana cara mengatasi keterbatasan data dalam pencarian nilai minimum fungsi objektif?
Apa strategi yang efektif untuk mengatasi fungsi non-konveks dalam pencarian nilai minimum?
Bagaimana cara menentukan nilai minimum fungsi objektif dengan batasan yang kompleks?
Bagaimana cara mengatasi masalah multi-objektif dalam pencarian nilai minimum?
Apa peran teknologi komputasi dalam mengatasi keterbatasan dan tantangan dalam pencarian nilai minimum fungsi objektif?