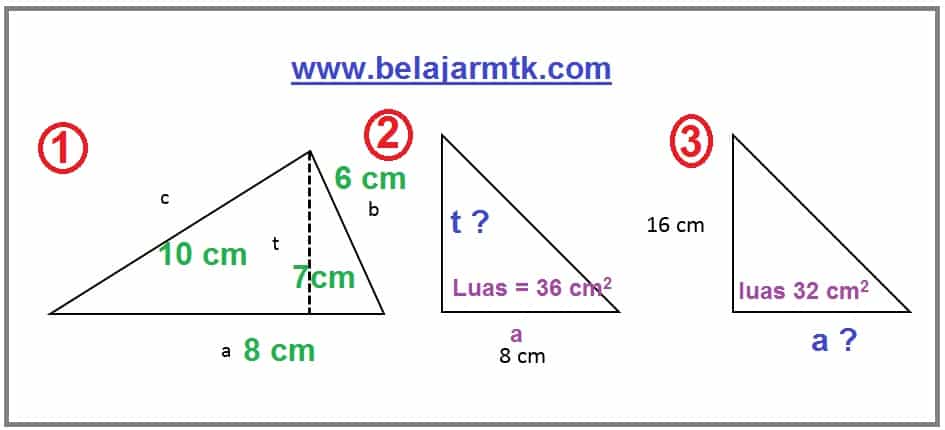
Luas segitiga ABC adalah area yang dibatasi oleh ketiga sisi segitiga tersebut. Menghitung luas segitiga merupakan salah satu konsep dasar dalam geometri yang sering kita jumpai dalam kehidupan sehari-hari. Bayangkan, ketika kita ingin menghitung luas tanah berbentuk segitiga atau menghitung jumlah cat yang dibutuhkan untuk mengecat dinding berbentuk segitiga, kita perlu memahami rumus luas segitiga.
Terdapat berbagai jenis segitiga, masing-masing memiliki ciri khas dan cara perhitungan luas yang berbeda. Kita akan mempelajari rumus luas segitiga dengan alas dan tinggi, rumus Heron untuk segitiga dengan tiga sisi, serta berbagai jenis segitiga dan penerapan luas segitiga dalam kehidupan sehari-hari.
Rumus Luas Segitiga
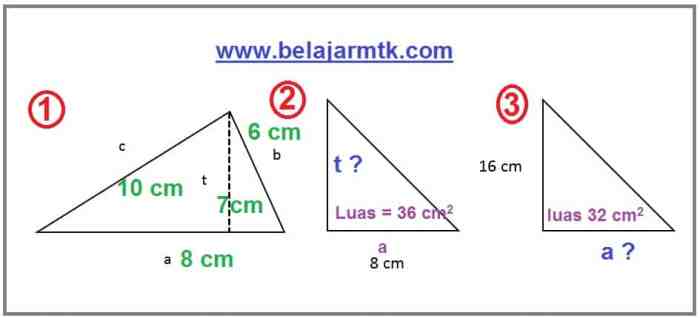
Segitiga merupakan bangun datar yang memiliki tiga sisi dan tiga sudut. Luas segitiga adalah ukuran area yang dipenuhi oleh segitiga tersebut. Ada beberapa rumus yang dapat digunakan untuk menghitung luas segitiga, tergantung pada informasi yang diketahui tentang segitiga tersebut.
Rumus Luas Segitiga dengan Alas dan Tinggi
Rumus luas segitiga dengan alas dan tinggi adalah:
Luas = 1/2 x alas x tinggi
Dimana:
- Alas adalah salah satu sisi segitiga yang dijadikan sebagai dasar perhitungan.
- Tinggi adalah garis tegak lurus dari titik sudut yang berhadapan dengan alas ke alas tersebut.
Contoh soal:
Hitunglah luas segitiga dengan alas 10 cm dan tinggi 6 cm!
Penyelesaian:
Luas = 1/2 x alas x tinggi
Luas = 1/2 x 10 cm x 6 cm
Luas = 30 cm2
Jadi, luas segitiga tersebut adalah 30 cm2.
Rumus Luas Segitiga dengan Tiga Sisi (Rumus Heron)
Rumus Heron digunakan untuk menghitung luas segitiga jika diketahui panjang ketiga sisinya. Rumus ini dikaitkan dengan ahli matematika Yunani, Heron dari Alexandria. Rumus Heron adalah:
Luas = √(s(s-a)(s-b)(s-c))
Dimana:
- a, b, dan c adalah panjang ketiga sisi segitiga.
- s adalah semiperimeter segitiga, yang dihitung dengan rumus s = (a + b + c) / 2.
Contoh soal:
Hitunglah luas segitiga dengan sisi a = 5 cm, b = 7 cm, dan c = 8 cm!
Penyelesaian:
s = (a + b + c) / 2
s = (5 cm + 7 cm + 8 cm) / 2
s = 10 cm
Luas = √(s(s-a)(s-b)(s-c))
Luas = √(10 cm (10 cm – 5 cm)(10 cm – 7 cm)(10 cm – 8 cm))
Luas = √(10 cm x 5 cm x 3 cm x 2 cm)
Luas = √(300 cm4)
Luas = 17.32 cm2 (dibulatkan ke dua desimal)
Jadi, luas segitiga tersebut adalah 17.32 cm2.
Jenis-jenis Segitiga
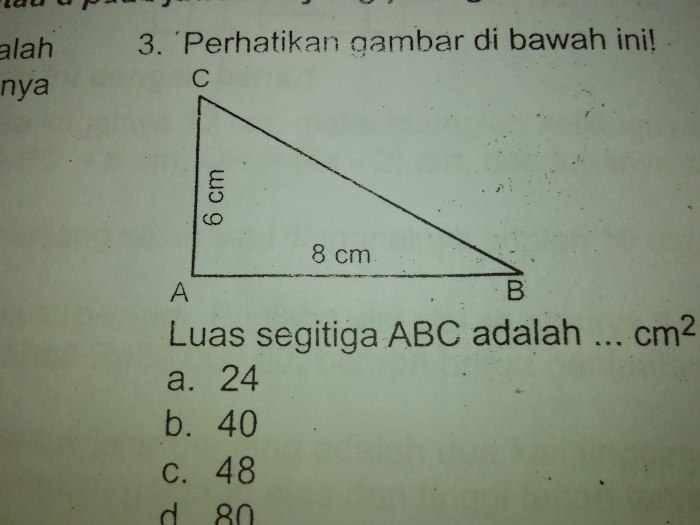
Segitiga merupakan bangun datar yang memiliki tiga sisi dan tiga sudut. Segitiga dapat diklasifikasikan berdasarkan sudut dan sisinya. Berdasarkan sudutnya, segitiga dapat dibagi menjadi tiga jenis, yaitu segitiga siku-siku, segitiga lancip, dan segitiga tumpul. Berdasarkan sisinya, segitiga dapat dibagi menjadi tiga jenis, yaitu segitiga sama sisi, segitiga sama kaki, dan segitiga sembarang.
Klasifikasi Segitiga Berdasarkan Sudut
Klasifikasi segitiga berdasarkan sudutnya memberikan gambaran tentang jenis sudut yang terdapat dalam segitiga tersebut. Berikut tabel yang merangkum klasifikasi segitiga berdasarkan sudut:
| Jenis Segitiga | Definisi | Gambar | Karakteristik |
|---|---|---|---|
| Segitiga Siku-siku | Segitiga yang memiliki satu sudut siku-siku (90 derajat). | Segitiga siku-siku memiliki satu sudut yang berukuran 90 derajat, dengan dua sudut lainnya yang berjumlah 90 derajat. Sisi yang berhadapan dengan sudut siku-siku disebut hipotenusa, dan sisi lainnya disebut kaki. |
|
| Segitiga Lancip | Segitiga yang memiliki ketiga sudutnya lancip (kurang dari 90 derajat). | Segitiga lancip memiliki ketiga sudutnya kurang dari 90 derajat. |
|
| Segitiga Tumpul | Segitiga yang memiliki satu sudut tumpul (lebih dari 90 derajat). | Segitiga tumpul memiliki satu sudut yang berukuran lebih dari 90 derajat, dengan dua sudut lainnya yang berjumlah kurang dari 90 derajat. |
|
Klasifikasi Segitiga Berdasarkan Sisi
Klasifikasi segitiga berdasarkan sisinya memberikan gambaran tentang panjang sisi-sisi yang menyusun segitiga tersebut. Berikut tabel yang merangkum klasifikasi segitiga berdasarkan sisi:
| Jenis Segitiga | Definisi | Gambar | Karakteristik |
|---|---|---|---|
| Segitiga Sama Sisi | Segitiga yang memiliki ketiga sisinya sama panjang. | Segitiga sama sisi memiliki ketiga sisinya sama panjang dan ketiga sudutnya sama besar (60 derajat). |
|
| Segitiga Sama Kaki | Segitiga yang memiliki dua sisinya sama panjang. | Segitiga sama kaki memiliki dua sisinya sama panjang dan dua sudutnya sama besar. |
|
| Segitiga Sembarang | Segitiga yang memiliki ketiga sisinya berbeda panjang. | Segitiga sembarang memiliki ketiga sisinya berbeda panjang dan ketiga sudutnya juga berbeda besar. |
|
Penerapan Luas Segitiga
Luas segitiga, yang dihitung dengan rumus setengah kali alas kali tinggi, memiliki banyak aplikasi dalam kehidupan sehari-hari. Konsep ini dapat digunakan untuk menghitung luas bidang datar lainnya, seperti persegi panjang, trapesium, dan bahkan bentuk yang lebih kompleks.
Soal Latihan: Luas Segitiga Abc Adalah

Setelah mempelajari rumus dan contoh perhitungan luas segitiga, mari kita berlatih dengan beberapa soal. Soal-soal berikut akan membantu Anda memahami konsep luas segitiga dengan lebih baik dan mengasah kemampuan Anda dalam menyelesaikan soal-soal yang berhubungan dengan luas segitiga.
Soal Latihan 1
Hitunglah luas segitiga ABC dengan alas 10 cm dan tinggi 8 cm.
Luas segitiga = 1/2 x alas x tinggi
Luas segitiga = 1/2 x 10 cm x 8 cm
Luas segitiga = 40 cm2
Soal Latihan 2
Sebuah segitiga memiliki alas 12 cm dan tinggi 5 cm. Hitunglah luas segitiga tersebut.
Luas segitiga = 1/2 x alas x tinggi
Luas segitiga = 1/2 x 12 cm x 5 cm
Luas segitiga = 30 cm2
Soal Latihan 3
Diketahui sebuah segitiga dengan alas 15 cm dan luasnya 45 cm2. Hitunglah tinggi segitiga tersebut.
Luas segitiga = 1/2 x alas x tinggi
45 cm2 = 1/2 x 15 cm x tinggi
tinggi = (45 cm2 x 2) / 15 cm
tinggi = 6 cm
Soal Latihan 4, Luas segitiga abc adalah
Sebuah segitiga sama sisi memiliki panjang sisi 8 cm. Hitunglah luas segitiga tersebut.
Luas segitiga sama sisi = (√3 / 4) x sisi2
Luas segitiga sama sisi = (√3 / 4) x 8 cm2
Luas segitiga sama sisi = 16√3 cm2
Soal Latihan 5
Sebuah segitiga siku-siku memiliki panjang sisi miring 10 cm dan salah satu sisi siku-sikunya 6 cm. Hitunglah luas segitiga tersebut.
Untuk menghitung luas segitiga siku-siku, kita perlu mengetahui panjang kedua sisi siku-sikunya. Kita dapat menggunakan teorema Pythagoras untuk mencari panjang sisi siku-siku lainnya.
Sisi miring2 = Sisi siku-siku 12 + Sisi siku-siku 22
10 cm2 = 6 cm2 + Sisi siku-siku 22
Sisi siku-siku 22 = 100 cm2 – 36 cm2
Sisi siku-siku 22 = 64 cm2
Sisi siku-siku 2 = 8 cm
Luas segitiga = 1/2 x alas x tinggi
Luas segitiga = 1/2 x 6 cm x 8 cm
Luas segitiga = 24 cm2