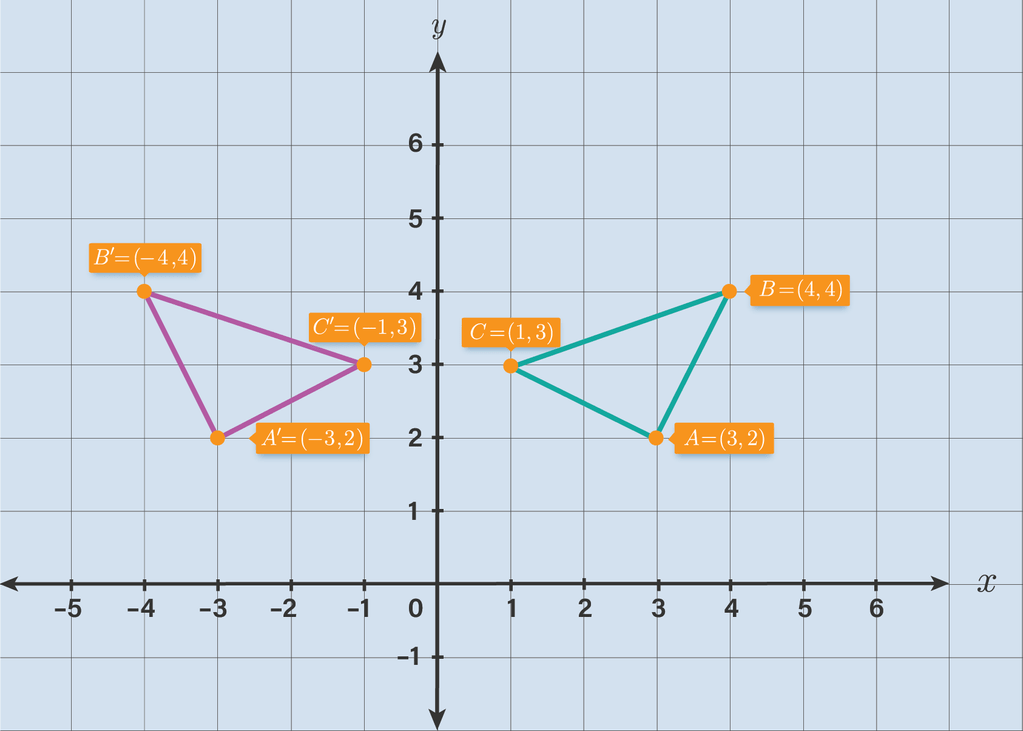
Diketahui segitiga abc yang titik sudutnya di a 3 2 – Bayangno, cak, segitiga ABC. Titik sudut A-ne wes ono, koordinat-e (3, 2). Sing penak, titik A iki bisa dadi titik awal kanggo nggambar segitiga ABC. Kira-kira, bentuk segitiga ABC-ne bakal kaya ngapa ya? Kalian penasaran? Ayo, kita telusuri bareng-bareng!
Dalam dunia geometri, segitiga ABC dengan titik sudut A (3, 2) iku duweni banyak kemungkinan bentuk. Titik A iku kaya titik acuan, titik sudut sing wis ditemtokno. Terus, titik sudut B lan C-ne piye? Kalian pengin ngerti hubungan antara titik sudut A lan sisi-sisi segitiga ABC? Atau malah ngitung luas lan keliling-e? Semuanya bakal kita bahas bareng-bareng!
Titik Sudut A
Kita akan membahas titik sudut A dalam segitiga ABC, yang memiliki koordinat (3, 2). Koordinat ini memberikan informasi tentang posisi titik A pada bidang kartesius, yaitu 3 satuan ke kanan dari sumbu Y dan 2 satuan ke atas dari sumbu X.
Koordinat Titik Sudut A
Titik sudut A memiliki koordinat (3, 2) dalam segitiga ABC. Ini berarti titik A terletak 3 satuan ke kanan dari sumbu Y dan 2 satuan ke atas dari sumbu X pada bidang kartesius.
Ilustrasi Titik Sudut A
Bayangkan sebuah bidang kartesius dengan sumbu X dan sumbu Y. Titik A terletak di titik potong garis vertikal yang melewati angka 3 pada sumbu X dan garis horizontal yang melewati angka 2 pada sumbu Y. Ini akan membentuk titik A dengan koordinat (3, 2).
Koordinat Titik Sudut B dan C
Untuk membentuk segitiga ABC, kita perlu menentukan koordinat titik sudut B dan C. Koordinat ini bisa berupa nilai apa saja, selama ketiga titik tidak terletak pada satu garis lurus.
| Titik Sudut | Koordinat X | Koordinat Y |
|---|---|---|
| A | 3 | 2 |
| B | 1 | 5 |
| C | 6 | 1 |
Contoh di atas menunjukkan satu kemungkinan kombinasi koordinat untuk titik B dan C. Kita dapat memilih kombinasi lain yang memenuhi syarat untuk membentuk segitiga.
Konsep Segitiga
Segitiga adalah bangun datar yang dibentuk oleh tiga ruas garis lurus yang saling berpotongan di tiga titik yang berbeda. Tiga titik potong tersebut disebut titik sudut segitiga, dan ruas garis yang menghubungkan dua titik sudut disebut sisi segitiga. Segitiga memiliki beberapa sifat dasar yang penting untuk dipahami, seperti jumlah sudut dalam segitiga selalu 180 derajat, dan jumlah panjang dua sisi segitiga selalu lebih besar dari panjang sisi ketiga.
Jenis-jenis Segitiga Berdasarkan Sudut
Segitiga dapat diklasifikasikan berdasarkan jenis sudut yang dibentuk oleh ketiga sisinya. Ada tiga jenis segitiga berdasarkan sudut:
- Segitiga Siku-siku: Segitiga yang memiliki satu sudut siku-siku (90 derajat). Sisi yang berhadapan dengan sudut siku-siku disebut sisi miring, dan sisi lainnya disebut sisi alas dan sisi tinggi. Contoh: Segitiga ABC dengan sudut siku-siku di B, dimana AB adalah sisi alas, BC adalah sisi tinggi, dan AC adalah sisi miring.
- Segitiga Lancip: Segitiga yang memiliki ketiga sudutnya lancip (kurang dari 90 derajat). Contoh: Segitiga DEF dengan sudut D, E, dan F semuanya kurang dari 90 derajat.
- Segitiga Tumpul: Segitiga yang memiliki satu sudut tumpul (lebih dari 90 derajat). Contoh: Segitiga GHI dengan sudut G lebih dari 90 derajat, sedangkan sudut H dan I kurang dari 90 derajat.
Jenis-jenis Segitiga Berdasarkan Sisi
Segitiga juga dapat diklasifikasikan berdasarkan panjang sisi-sisinya. Ada tiga jenis segitiga berdasarkan sisi:
- Segitiga Sama Sisi: Segitiga yang memiliki ketiga sisinya sama panjang. Contoh: Segitiga JKL dengan panjang sisi JK, KL, dan LJ yang sama.
- Segitiga Sama Kaki: Segitiga yang memiliki dua sisinya sama panjang. Contoh: Segitiga MNO dengan panjang sisi MN dan MO yang sama, sedangkan sisi NO berbeda.
- Segitiga Sembarang: Segitiga yang memiliki ketiga sisinya berbeda panjang. Contoh: Segitiga PQR dengan panjang sisi PQ, QR, dan RP yang berbeda.
Contoh Ilustrasi Berbagai Jenis Segitiga
Berikut adalah ilustrasi yang menunjukkan berbagai jenis segitiga berdasarkan sudut dan sisi:
| Jenis Segitiga | Ilustrasi | Keterangan |
| Segitiga Siku-siku | [Gambar segitiga siku-siku dengan sisi miring, alas, dan tinggi yang diberi label] | Segitiga ABC dengan sudut siku-siku di B, AB adalah sisi alas, BC adalah sisi tinggi, dan AC adalah sisi miring. |
| Segitiga Lancip | [Gambar segitiga lancip dengan ketiga sudutnya diberi label] | Segitiga DEF dengan sudut D, E, dan F semuanya kurang dari 90 derajat. |
| Segitiga Tumpul | [Gambar segitiga tumpul dengan sudut tumpul dan sudut lancip yang diberi label] | Segitiga GHI dengan sudut G lebih dari 90 derajat, sedangkan sudut H dan I kurang dari 90 derajat. |
| Segitiga Sama Sisi | [Gambar segitiga sama sisi dengan ketiga sisinya diberi label] | Segitiga JKL dengan panjang sisi JK, KL, dan LJ yang sama. |
| Segitiga Sama Kaki | [Gambar segitiga sama kaki dengan dua sisinya yang sama panjang diberi label] | Segitiga MNO dengan panjang sisi MN dan MO yang sama, sedangkan sisi NO berbeda. |
| Segitiga Sembarang | [Gambar segitiga sembarang dengan ketiga sisinya diberi label] | Segitiga PQR dengan panjang sisi PQ, QR, dan RP yang berbeda. |
Hubungan Titik Sudut dan Sisi
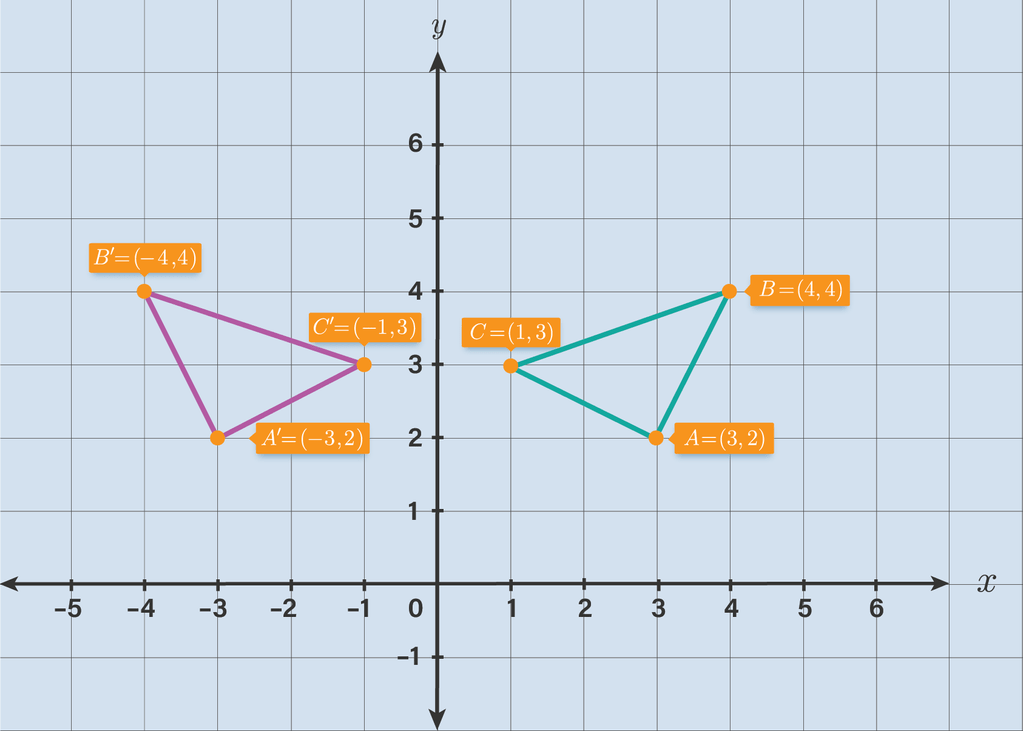
Segitiga ABC, dengan titik sudut A di (3, 2), memiliki hubungan yang erat antara titik sudut dan sisi-sisi yang membentuknya. Hubungan ini penting untuk memahami karakteristik dan sifat segitiga, serta untuk melakukan berbagai operasi geometri pada segitiga tersebut.
Sisi-Sisi yang Berdekatan dengan Titik Sudut A
Titik sudut A adalah titik pertemuan dari dua sisi segitiga, yaitu sisi AB dan sisi AC. Sisi-sisi ini disebut sebagai sisi yang berdekatan dengan titik sudut A.
Sisi-sisi yang berdekatan dengan titik sudut A adalah sisi AB dan sisi AC.
Dalam konteks geometri, sisi-sisi yang berdekatan dengan titik sudut A merupakan sisi yang membentuk sudut A.
Ilustrasi Hubungan Titik Sudut A dan Sisi-Sisi Segitiga
Bayangkan segitiga ABC dengan titik sudut A di (3, 2). Titik A adalah titik pertemuan antara sisi AB dan sisi AC.
Misalkan titik B terletak di (1, 4) dan titik C terletak di (5, 1). Sisi AB akan menghubungkan titik A (3, 2) dan titik B (1, 4). Sementara itu, sisi AC akan menghubungkan titik A (3, 2) dan titik C (5, 1).
Ilustrasi ini menunjukkan bagaimana titik sudut A berperan sebagai titik pertemuan dua sisi yang membentuk sudut A.
Kemungkinan Bentuk Segitiga ABC
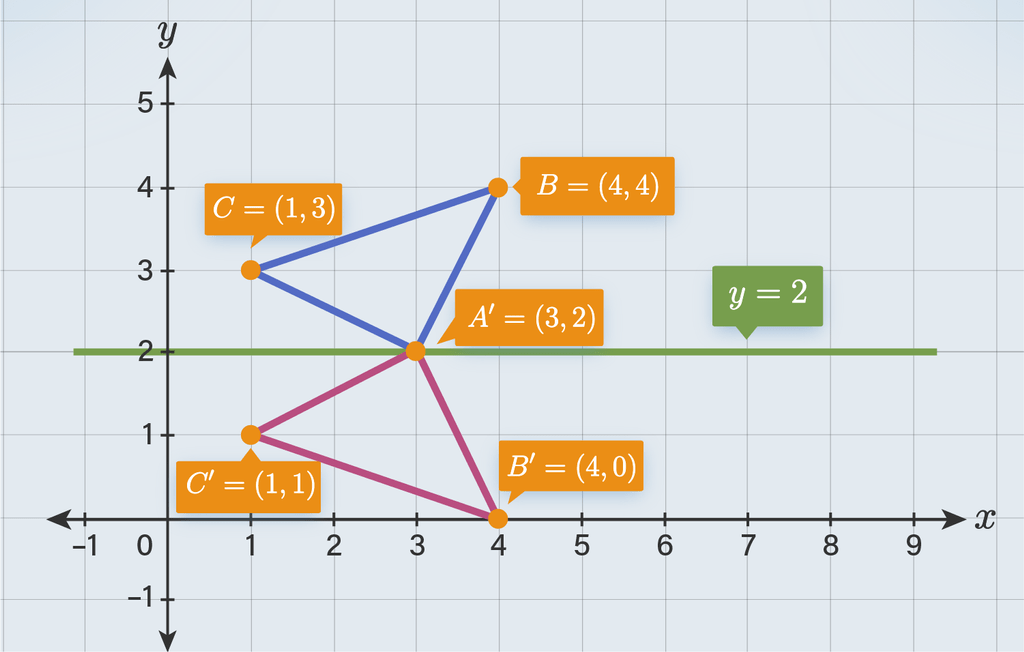
Setelah mengetahui titik sudut A (3, 2) pada segitiga ABC, kita dapat mengeksplorasi berbagai kemungkinan bentuk segitiga yang dapat dibentuk. Posisi titik A ini memberikan kita titik acuan untuk menentukan kemungkinan posisi titik B dan C, yang akan menentukan bentuk akhir segitiga ABC.
Kemungkinan Bentuk Segitiga ABC
Berdasarkan koordinat titik A (3, 2), segitiga ABC dapat memiliki berbagai bentuk, seperti segitiga siku-siku, segitiga sama kaki, segitiga sama sisi, segitiga lancip, dan segitiga tumpul.
Ilustrasi Kemungkinan Bentuk Segitiga ABC
Untuk memperjelas, mari kita perhatikan beberapa ilustrasi yang menunjukkan kemungkinan bentuk segitiga ABC dengan titik A (3, 2) sebagai titik acuan:
- Segitiga Siku-siku: Titik B dan C dapat ditempatkan sedemikian rupa sehingga salah satu sudut segitiga ABC bernilai 90 derajat. Misalnya, titik B dapat berada di (3, 0) dan titik C di (5, 2), membentuk segitiga siku-siku dengan sudut siku-siku di titik A.
- Segitiga Sama Kaki: Titik B dan C dapat ditempatkan sedemikian rupa sehingga dua sisi segitiga ABC memiliki panjang yang sama. Misalnya, titik B dapat berada di (1, 2) dan titik C di (5, 2), membentuk segitiga sama kaki dengan sisi AB dan AC yang sama panjang.
- Segitiga Sama Sisi: Titik B dan C dapat ditempatkan sedemikian rupa sehingga ketiga sisi segitiga ABC memiliki panjang yang sama. Misalnya, titik B dapat berada di (1, 2 + √3) dan titik C di (3 + √3, 2), membentuk segitiga sama sisi dengan panjang sisi yang sama.
- Segitiga Lancip: Titik B dan C dapat ditempatkan sedemikian rupa sehingga ketiga sudut segitiga ABC kurang dari 90 derajat. Misalnya, titik B dapat berada di (2, 1) dan titik C di (4, 3), membentuk segitiga lancip.
- Segitiga Tumpul: Titik B dan C dapat ditempatkan sedemikian rupa sehingga salah satu sudut segitiga ABC lebih besar dari 90 derajat. Misalnya, titik B dapat berada di (0, 2) dan titik C di (6, 2), membentuk segitiga tumpul dengan sudut tumpul di titik A.
Tabel Kemungkinan Bentuk Segitiga ABC
| Bentuk Segitiga | Karakteristik | Contoh Koordinat B dan C |
|---|---|---|
| Siku-siku | Salah satu sudut bernilai 90 derajat | B (3, 0), C (5, 2) |
| Sama Kaki | Dua sisi memiliki panjang yang sama | B (1, 2), C (5, 2) |
| Sama Sisi | Ketiga sisi memiliki panjang yang sama | B (1, 2 + √3), C (3 + √3, 2) |
| Lancip | Ketiga sudut kurang dari 90 derajat | B (2, 1), C (4, 3) |
| Tumpul | Salah satu sudut lebih besar dari 90 derajat | B (0, 2), C (6, 2) |
Perhitungan Luas dan Keliling: Diketahui Segitiga Abc Yang Titik Sudutnya Di A 3 2

Setelah mengetahui koordinat titik sudut A (3, 2), kita perlu mengetahui koordinat titik sudut B dan C untuk menghitung luas dan keliling segitiga ABC. Dengan koordinat titik sudut B dan C, kita dapat menggunakan rumus dan langkah-langkah perhitungan yang tepat untuk menentukan luas dan keliling segitiga.
Cara Menghitung Luas dan Keliling Segitiga
Untuk menghitung luas dan keliling segitiga ABC, kita perlu menentukan panjang sisi-sisi segitiga tersebut. Berikut adalah cara menghitungnya:
- Menghitung Panjang Sisi: Gunakan rumus jarak antara dua titik untuk menghitung panjang sisi-sisi segitiga ABC. Misalnya, untuk menghitung panjang sisi AB, kita dapat menggunakan rumus jarak antara titik A (3, 2) dan titik B (xB, yB).
- Menghitung Luas: Setelah mengetahui panjang ketiga sisi segitiga, kita dapat menggunakan rumus Heron untuk menghitung luasnya. Rumus Heron menyatakan bahwa luas segitiga sama dengan akar kuadrat dari hasil kali semiperimeter dengan selisih semiperimeter dan ketiga sisi segitiga.
- Menghitung Keliling: Keliling segitiga ABC adalah jumlah panjang ketiga sisinya.
Contoh Perhitungan Luas dan Keliling Segitiga
Misalkan koordinat titik sudut B adalah (5, 4) dan koordinat titik sudut C adalah (1, 6). Berikut adalah contoh perhitungan luas dan keliling segitiga ABC:
- Menghitung Panjang Sisi:
- AB = √[(5 – 3)2 + (4 – 2)2] = √(22 + 22) = √8 = 2√2
- BC = √[(1 – 5)2 + (6 – 4)2] = √((-4)2 + 22) = √20 = 2√5
- AC = √[(1 – 3)2 + (6 – 2)2] = √((-2)2 + 42) = √20 = 2√5
- Menghitung Luas:
- Semiperimeter (s) = (AB + BC + AC) / 2 = (2√2 + 2√5 + 2√5) / 2 = √2 + √5 + √5 = √2 + 2√5
- Luas = √[s(s – AB)(s – BC)(s – AC)] = √[(√2 + 2√5)(√2 + 2√5 – 2√2)(√2 + 2√5 – 2√5)(√2 + 2√5 – 2√5)] = √[(√2 + 2√5)(-√2 + 2√5)(√2)(√2)] = √[(-2 + 20)(2)] = √36 = 6 satuan luas
- Menghitung Keliling:
- Keliling = AB + BC + AC = 2√2 + 2√5 + 2√5 = 2√2 + 4√5 satuan panjang
Demonstrasi Penggunaan Rumus dan Langkah-langkah Perhitungan, Diketahui segitiga abc yang titik sudutnya di a 3 2
Dalam contoh di atas, kita telah menggunakan rumus jarak antara dua titik untuk menghitung panjang sisi-sisi segitiga. Kemudian, kita menggunakan rumus Heron untuk menghitung luas segitiga. Terakhir, kita menjumlahkan panjang ketiga sisi untuk menghitung keliling segitiga.
Langkah-langkah perhitungan ini dapat diterapkan pada segitiga ABC dengan koordinat titik sudut B dan C yang berbeda. Pastikan untuk menggunakan rumus yang tepat dan mengikuti langkah-langkah dengan benar untuk mendapatkan hasil yang akurat.