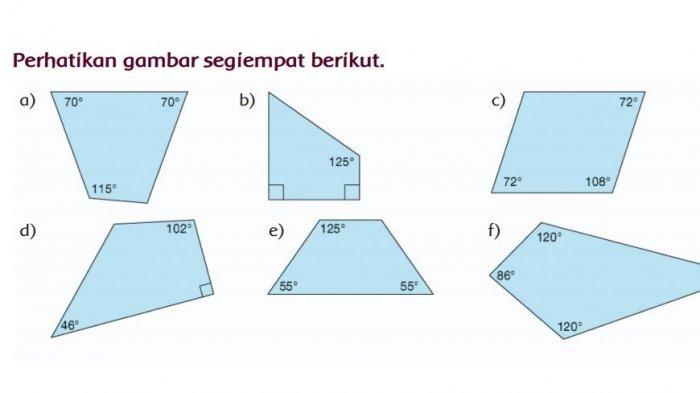
Coba bayangin, lagi ngerjain tugas matematika, eh tiba-tiba ketemu soal tentang sudut. “Besar sudut N pada bangun berikut adalah…?” Waduh, bingung kan? Tenang, ga usah panik dulu! Yuk, kita bahas bareng-bareng tentang sudut, mulai dari pengertiannya sampai cara ngitungnya. Biar kamu ga lagi pusing ngerjain soal-soal yang berhubungan dengan sudut.
Sudut itu kaya gini, lho. Bayangin kamu lagi nggambar di kertas. Nah, garis yang kamu gambar itu membentuk sudut, lho! Ada berbagai macam sudut, mulai dari sudut lancip, sudut siku-siku, sudut tumpul, sampai sudut refleks. Setiap sudut punya ciri khas masing-masing yang bisa kamu kenali dengan mudah. Terus, gimana cara ngitung besar sudutnya? Nah, itu dia yang bakal kita pelajari bareng-bareng.
Mengenal Sudut: Besar Sudut N Pada Bangun Berikut Adalah
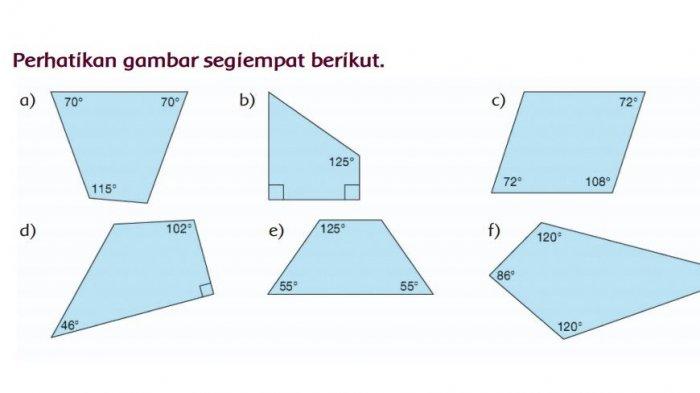
Sudut merupakan salah satu konsep dasar dalam geometri yang sering kita temui dalam kehidupan sehari-hari. Sudut terbentuk dari pertemuan dua garis lurus yang memiliki titik perpotongan. Dalam geometri, sudut diukur dalam satuan derajat (°). Sudut memiliki peran penting dalam berbagai bidang, seperti arsitektur, teknik, navigasi, dan seni.
Contoh Sudut dalam Kehidupan Sehari-hari
Sudut hadir di mana-mana di sekitar kita. Berikut beberapa contohnya:
- Pintu: Ketika pintu terbuka, membentuk sudut antara daun pintu dan kusen.
- Jam: Jarum jam dan jarum menit membentuk sudut pada jam analog.
- Bangunan: Sudut dibentuk oleh pertemuan dinding dan atap rumah, atau sudut-sudut pada bentuk geometris bangunan.
- Trafik: Tanda-tanda lalu lintas, seperti rambu stop, menunjukkan sudut yang berbeda untuk menginformasikan pengemudi.
- Seni: Sudut digunakan dalam seni lukis dan desain untuk menciptakan perspektif dan komposisi.
Jenis-jenis Sudut, Besar sudut n pada bangun berikut adalah
Berdasarkan besarnya, sudut diklasifikasikan menjadi beberapa jenis, yaitu:
| Jenis Sudut | Ciri Khas | Contoh |
|---|---|---|
| Sudut Lancip | Berukuran kurang dari 90° | Sudut yang dibentuk oleh jarum jam pada pukul 02.00 |
| Sudut Siku-siku | Berukuran tepat 90° | Sudut yang dibentuk oleh pertemuan dua sisi persegi panjang |
| Sudut Tumpul | Berukuran lebih dari 90° tetapi kurang dari 180° | Sudut yang dibentuk oleh jarum jam pada pukul 04.00 |
| Sudut Refleks | Berukuran lebih dari 180° tetapi kurang dari 360° | Sudut yang dibentuk oleh jarum jam pada pukul 10.00 |
Menentukan Sudut pada Bangun Datar
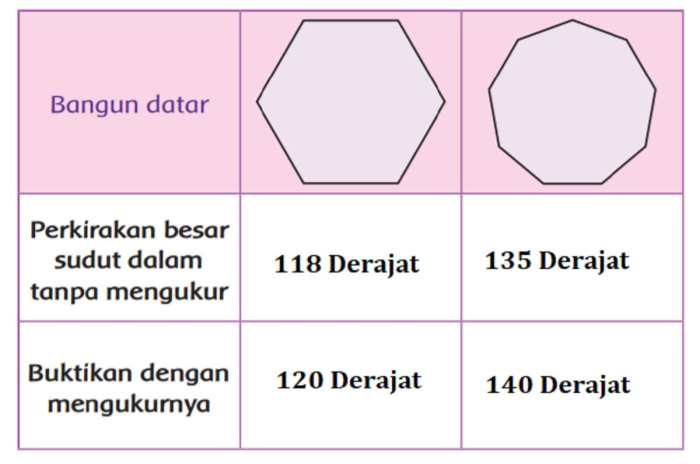
Menentukan besar sudut pada bangun datar merupakan langkah penting dalam geometri. Dengan memahami cara menentukan sudut, kita dapat menganalisis dan menyelesaikan berbagai masalah terkait bangun datar, seperti menghitung luas dan keliling, serta menentukan hubungan antar sisi dan sudut.
Cara Menentukan Besar Sudut pada Bangun Datar
Cara menentukan besar sudut pada bangun datar tergantung pada jenis bangunnya. Berikut beberapa cara yang umum digunakan:
- Segitiga: Jumlah sudut dalam segitiga selalu 180 derajat. Untuk menentukan besar sudut pada segitiga, kita dapat menggunakan rumus:
Sudut A + Sudut B + Sudut C = 180 derajat
- Persegi Panjang: Persegi panjang memiliki empat sudut siku-siku, yang masing-masing berukuran 90 derajat.
- Lingkaran: Lingkaran tidak memiliki sudut, tetapi kita dapat menentukan besar sudut yang dibentuk oleh dua jari-jari lingkaran yang bertemu di pusat lingkaran. Besar sudut ini sama dengan besar busur lingkaran yang diapit oleh kedua jari-jari tersebut.
Contoh Perhitungan Sudut pada Segitiga
Misalnya, kita memiliki segitiga ABC dengan besar sudut A = 60 derajat dan sudut B = 80 derajat. Untuk menentukan besar sudut C, kita dapat menggunakan rumus jumlah sudut dalam segitiga:
Sudut A + Sudut B + Sudut C = 180 derajat
60 derajat + 80 derajat + Sudut C = 180 derajat
Sudut C = 180 derajat – 60 derajat – 80 derajat
Sudut C = 40 derajat
Jadi, besar sudut C pada segitiga ABC adalah 40 derajat.
Ilustrasi Perhitungan Sudut pada Segitiga
Berikut ilustrasi segitiga ABC dengan sudut A = 60 derajat, sudut B = 80 derajat, dan sudut C = 40 derajat:
Gambar segitiga ABC dengan sudut A, B, dan C. Sudut A ditandai dengan tanda busur kecil di dekat titik sudut A, sudut B dengan tanda busur kecil di dekat titik sudut B, dan sudut C dengan tanda busur kecil di dekat titik sudut C. Sudut A berukuran 60 derajat, sudut B berukuran 80 derajat, dan sudut C berukuran 40 derajat.
Dalam ilustrasi ini, kita dapat melihat bahwa jumlah ketiga sudut dalam segitiga ABC adalah 180 derajat (60 derajat + 80 derajat + 40 derajat = 180 derajat). Ini membuktikan bahwa rumus jumlah sudut dalam segitiga berlaku untuk semua segitiga.
Menentukan Sudut pada Bangun Ruang
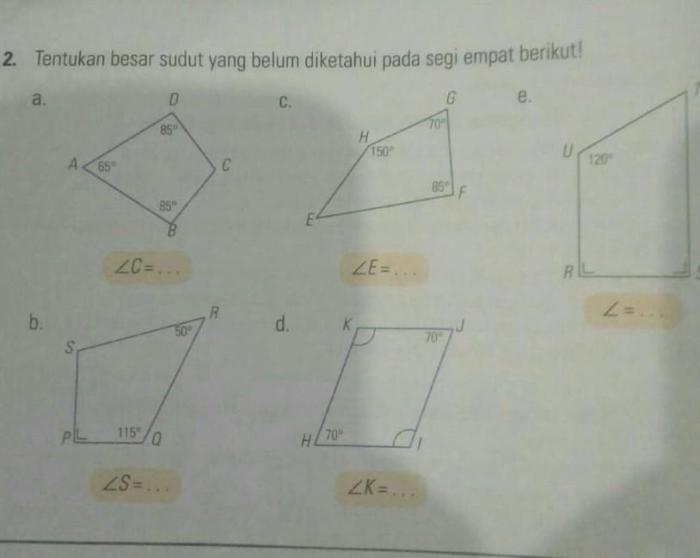
Menentukan besar sudut pada bangun ruang seperti kubus, balok, dan limas merupakan hal penting dalam memahami geometri ruang. Bangun ruang memiliki berbagai jenis sudut, seperti sudut siku-siku, sudut lancip, dan sudut tumpul. Mempelajari cara menentukan besar sudut pada bangun ruang akan membantu kita dalam memahami dan menyelesaikan berbagai masalah geometri yang lebih kompleks.
Cara Menentukan Besar Sudut pada Bangun Ruang
Untuk menentukan besar sudut pada bangun ruang, kita dapat menggunakan beberapa metode, di antaranya:
- Menggunakan rumus jumlah sudut dalam bangun datar: Bangun ruang tersusun dari bangun datar, seperti persegi, persegi panjang, segitiga, dan lain-lain. Kita dapat memanfaatkan rumus jumlah sudut dalam bangun datar tersebut untuk menentukan besar sudut pada bangun ruang.
- Menggunakan teorema Pythagoras: Teorema Pythagoras dapat digunakan untuk menentukan panjang sisi-sisi segitiga siku-siku yang terdapat pada bangun ruang. Dengan mengetahui panjang sisi-sisi segitiga siku-siku, kita dapat menentukan besar sudutnya.
- Menggunakan trigonometri: Trigonometri dapat digunakan untuk menentukan besar sudut pada bangun ruang dengan menggunakan perbandingan sisi-sisi segitiga siku-siku.
Contoh Perhitungan Sudut pada Balok
Sebagai contoh, kita akan menghitung besar sudut pada balok. Balok tersusun dari enam persegi panjang. Kita dapat menggunakan rumus jumlah sudut dalam persegi panjang untuk menentukan besar sudut pada setiap titik sudutnya.
Misalnya, kita memiliki balok dengan panjang, lebar, dan tinggi masing-masing 6 cm, 4 cm, dan 3 cm. Titik sudut A pada balok tersebut merupakan titik pertemuan antara tiga persegi panjang. Kita dapat menentukan besar sudut pada titik A dengan menggunakan rumus jumlah sudut dalam persegi panjang.
Jumlah sudut dalam persegi panjang = 360 derajat
Titik A merupakan titik pertemuan antara tiga persegi panjang, yaitu ABCD, ABFE, dan ADHE. Sudut pada titik A adalah sudut BAC, sudut BAE, dan sudut DAE. Kita dapat menentukan besar sudut BAC dengan menggunakan rumus jumlah sudut dalam persegi panjang ABCD.
Sudut BAC = 360 derajat – sudut ABC – sudut CDA = 360 derajat – 90 derajat – 90 derajat = 180 derajat
Dengan cara yang sama, kita dapat menentukan besar sudut BAE dan sudut DAE. Sehingga, besar sudut pada titik A adalah 180 derajat untuk setiap sudut.
Ilustrasi:
Gambar balok dengan titik sudut A, B, C, D, E, F, G, dan H. Titik A merupakan titik pertemuan antara tiga persegi panjang, yaitu ABCD, ABFE, dan ADHE. Titik A terletak di sudut atas balok. Titik B, C, D, E, F, G, dan H terletak pada titik sudut lainnya.
Sudut BAC, BAE, dan DAE merupakan sudut yang terbentuk pada titik A. Sudut ABC, CDA, ABE, AFE, ADE, dan DHE merupakan sudut yang terbentuk pada titik sudut lainnya. Besar sudut pada setiap titik sudut dapat dihitung dengan menggunakan rumus jumlah sudut dalam persegi panjang.
Penerapan Sudut dalam Kehidupan Sehari-hari
Sudut, konsep dasar dalam geometri, ternyata memiliki peran penting dalam kehidupan sehari-hari. Mulai dari bangunan megah hingga karya seni yang memukau, sudut berperan dalam menentukan bentuk, struktur, dan estetika. Tanpa sudut, dunia kita akan tampak berbeda dan mungkin kurang fungsional.
Arsitektur
Dalam arsitektur, sudut merupakan elemen fundamental yang menentukan bentuk dan stabilitas bangunan. Sudut-sudut yang tepat memastikan keseimbangan struktur dan kekuatan bangunan. Sudut siku-siku (90 derajat) sering digunakan dalam konstruksi bangunan untuk menciptakan sudut yang kuat dan stabil. Misalnya, pada desain rumah, sudut siku-siku digunakan untuk membentuk dinding dan langit-langit yang kokoh. Sudut-sudut lain, seperti sudut lancip (kurang dari 90 derajat) dan sudut tumpul (lebih dari 90 derajat), juga digunakan untuk menciptakan desain yang unik dan menarik.
Desain
Dalam desain, sudut berperan dalam menciptakan proporsi, keseimbangan, dan estetika. Sudut yang tepat dapat menciptakan ilusi optik, seperti membuat ruangan tampak lebih luas atau lebih tinggi. Sudut juga dapat digunakan untuk membagi ruang menjadi area yang berbeda, menciptakan fokus pada elemen tertentu, dan memberikan karakter pada desain.
- Sudut lancip dapat memberikan kesan dinamis dan energik, sering digunakan dalam desain modern.
- Sudut tumpul dapat menciptakan kesan elegan dan klasik, sering digunakan dalam desain tradisional.
- Sudut siku-siku dapat memberikan kesan kuat dan stabil, sering digunakan dalam desain minimalis.
Seni
Dalam seni, sudut berperan dalam menciptakan perspektif, komposisi, dan ekspresi. Seniman menggunakan sudut untuk menciptakan ilusi kedalaman, membimbing mata penonton, dan menyampaikan emosi. Sudut juga dapat digunakan untuk menciptakan bentuk dan tekstur yang unik.
- Dalam lukisan perspektif, sudut digunakan untuk menciptakan ilusi kedalaman dan ruang tiga dimensi.
- Dalam seni abstrak, sudut dapat digunakan untuk menciptakan bentuk dan komposisi yang tidak konvensional.
- Dalam seni patung, sudut digunakan untuk menciptakan bentuk dan volume yang unik.
Contoh Penerapan Sudut
| Bidang | Contoh | Penjelasan |
|---|---|---|
| Arsitektur | Bangunan dengan atap miring | Sudut atap miring membantu mengalirkan air hujan dan memberikan stabilitas struktur. |
| Desain | Meja dengan sudut tumpul | Sudut tumpul pada meja menciptakan kesan elegan dan nyaman. |
| Seni | Lukisan dengan perspektif | Sudut dalam lukisan perspektif menciptakan ilusi kedalaman dan ruang tiga dimensi. |
| Teknik | Gergaji dengan sudut tajam | Sudut tajam pada gergaji membantu memotong kayu dengan lebih mudah dan presisi. |
| Matematika | Trigonometri | Trigonometri menggunakan sudut untuk menghitung panjang sisi dan besar sudut dalam segitiga. |